As-rigid-as-possible shape interpolationについて解説をする

2019年08月17日

SIGGRAPH 2000の論文、「As-rigid-as-possible shape interpolation」についての解説を書きます。間違いや不正確な内容などがありましたらTwitterまで連絡をお願いします。

「As-rigid-as-possible shape interpolation」は２次元の三角形メッシュのインターポレーションを行う手法の提案論文です。この手法で次のようなメッシュのインターポレーションが行なえます。

As Rigid As Possible Shape Interpolation実装できた。二次元のトポロジが同じ頂点の対応付けがなされたメッシュ2つの間の補間を行う手法。 pic.twitter.com/9Hbdx7Cmow
— 折登いつき (@MatchaChoco010) June 2, 2019

無駄にドロネー三角形分割実装しているのでポチポチやってメッシュを作れます。 pic.twitter.com/LUsq7CArEa
— 折登いつき (@MatchaChoco010) June 2, 2019

楽しい pic.twitter.com/FJxgoAaj5r
— 折登いつき (@MatchaChoco010) June 2, 2019

早速論文の手法を解説していきます。

この論文で扱うメッシュとは2次元の三角形の集合体です。

2019 08 17 14 40 07

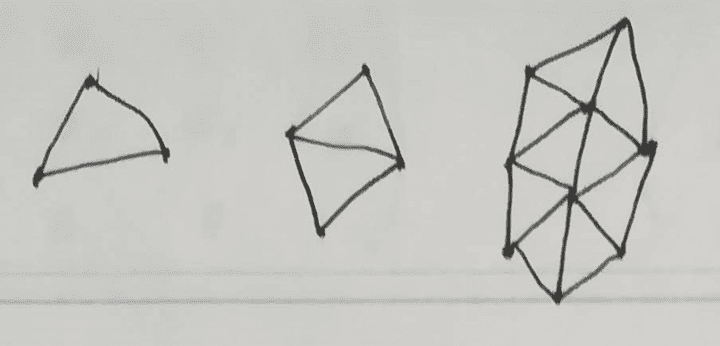
まずはメッシュについて扱う前に三角形一枚について考えます。三角形 $P (p_0, p_1, p_2)$ と $Q (q_0, q_1, q_2)$ が与えられたとします。

2019 08 17 14 40 41

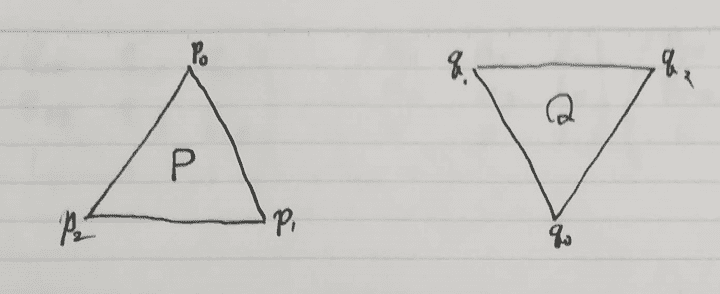
三角形同士を補間するということで一番最初に思いつくのは各頂点の座標を線形補間することだと思います。しかし頂点の座標をそのまま線形補間する場合、三角形が縮んでしまうなどの問題があります。

2019 08 17 14 41 57

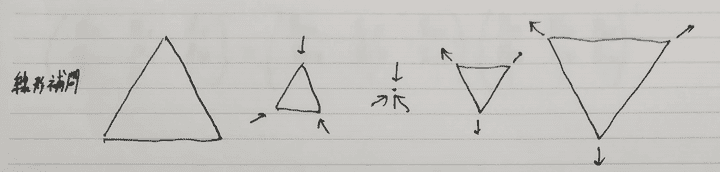
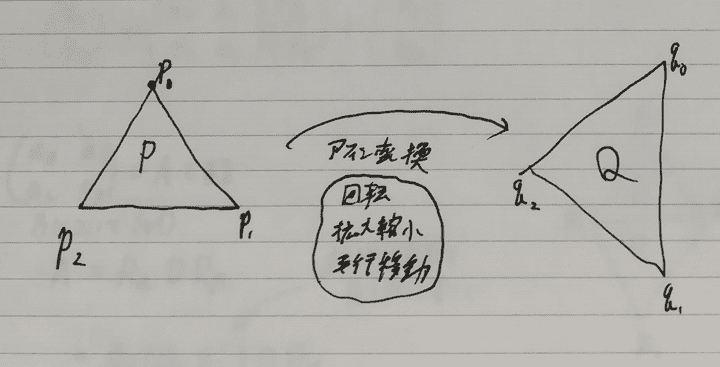
三角形が回転するように変形してほしいわけですが、そのような変形について考えていきます。

2019 08 17 14 42 19

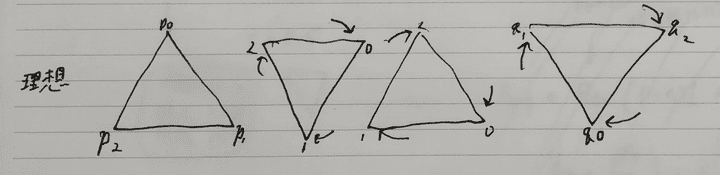
まず最初にPからQへのアフィン変換を計算します。 PからQへのアフィン変換(平行移動、回転、拡大縮小が合わさったもの)は必ず計算できます。

2019 08 17 14 43 14

2019 08 17 14 43 23

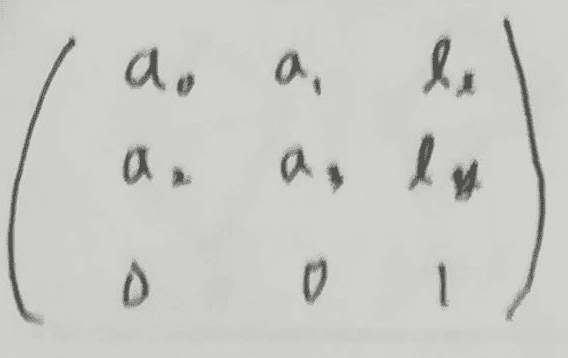
2次元なのに3次の行列なのは同次座標系を扱うからです。

点p0の座標を $(p_{0x}, p_{0y})$ というふうに表記するとします。するとアフィン変換で次のように書けます。

2019 08 17 14 44 20

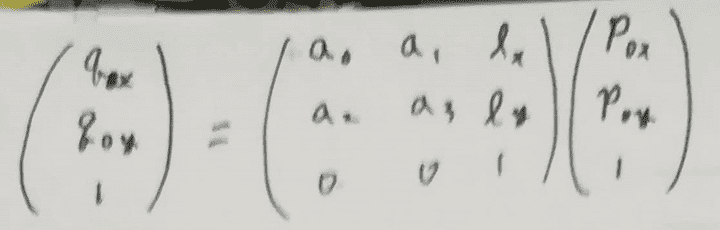
頂点3つをまとめて書くと次のようになります。

2019 08 17 14 44 35

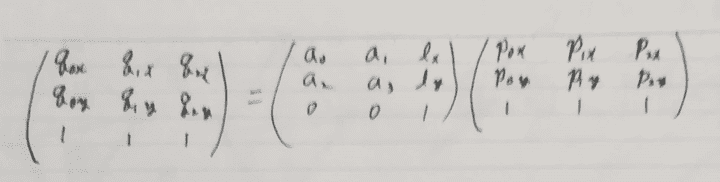
ここからアフィン変換は次のように求められます。

2019 08 17 14 44 49

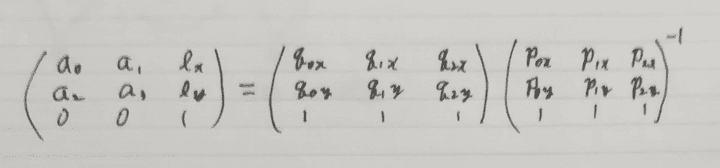
degenerateしていなければ(頂点2つあるいは3つが同一の点とならなければ)、つまり三角形であれば逆行列は存在します。

三角形Pから三角形Qへのアフィン変換が求まりました。ここから、時刻tのときの三角形の形状を次のように定めます。

アフィン変換を平行移動と拡大縮小と回転に分解し、平行移動成分と拡大縮小成分については線形補間、回転は回転角thetaについて線形補間してそれらを組み合わせたもの。

例えばPからQへのアフィン変換が x方向に10、y方向に20平行移動し、 x方向に2倍、y方向に2倍拡大され、 90度回転するものだったとします。このとき、時刻t=0.5では、 x方向に5、y方向に10平行移動し、 x方向に1.5倍、y方向に1.5倍拡大され、 45度回転したアフィン変換とします。

2019 08 17 14 45 54

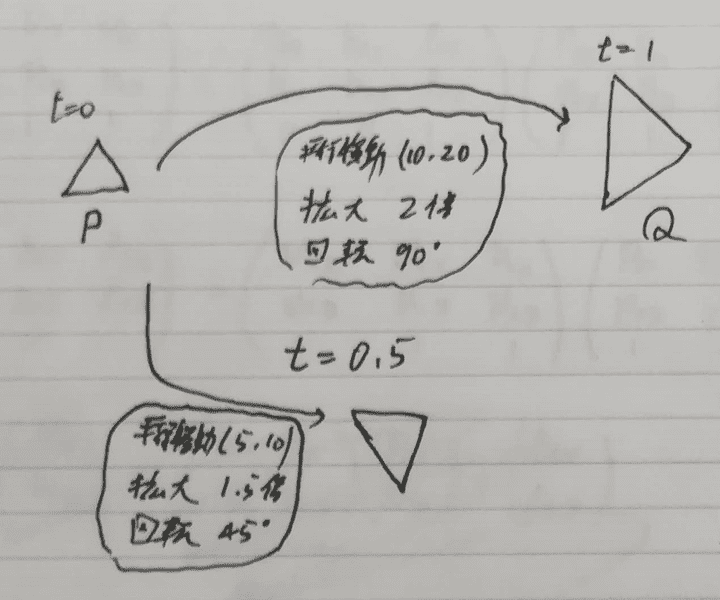
アフィン変換を平行移動と拡大縮小、回転成分に分解するには次のようにします。

まずは平行移動成分を分解します。平行移動成分は行列で回転や拡大縮小と別の要素になっているので簡単に分解できます。次の式は3x3ではなくて2x2の表現にしています。

2019 08 17 14 46 21

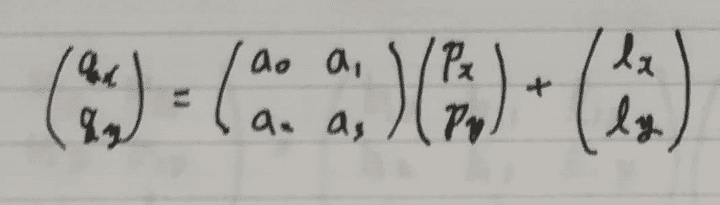
次に、回転と拡大縮小が合わさった(a0, a1; a2, a3)について特異値分解します。特異値分解した左側と右側の要素は直交行列なことに注意して次のように変形します。

2019 08 17 14 46 45

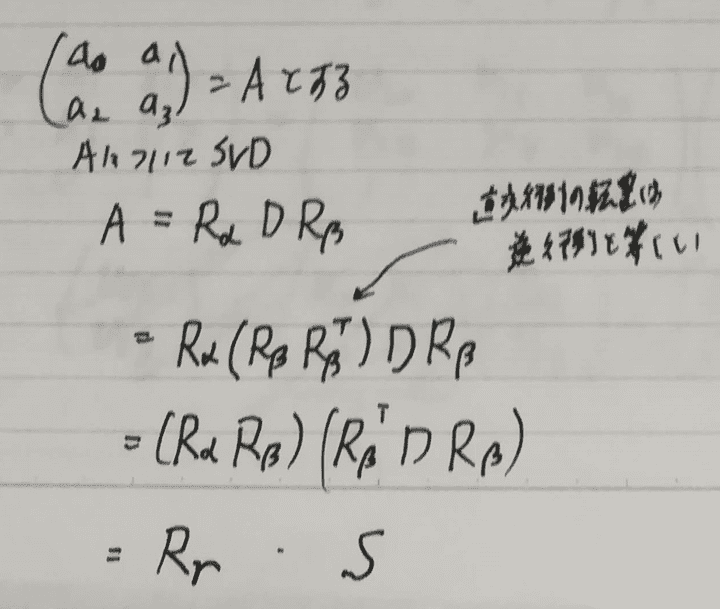
このとき、 $R_{\gamma}$ は回転行列になることは証明されているようです。 Sは厳密には拡大縮小のほかにせん断も含みます。

回転行列とそれ以外に分解するというとQR分解ベースのものもあるらしいですが、論文によれば今回の場合はSVDベースのほうが良い結果になるらしいです。

時刻ｔでの望ましいアフィン変換の回転と拡大成分を次のようにしてAという行列で表現できます。

2019 08 17 14 47 53

さて、三角形一枚の場合については上記のようにして最適な変形を求めることができました。

次に三角形二枚以上の場合について考えます。

2019 08 17 14 48 12

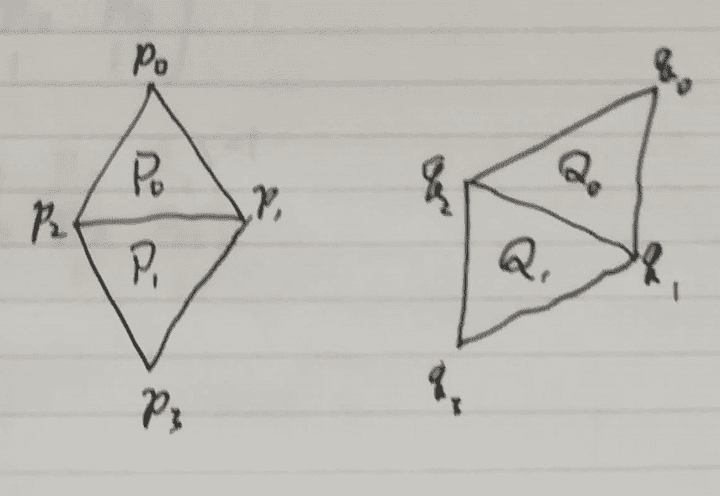
上図は三角形が二枚組み合わさったものです。

それぞれの三角形について最適なアフィン変換が求まります。

しかし、このアフィン変換はそのまま使えません。 t=0とt=1の場合には2つの三角形の共有する頂点が一致しますが、それ以外の場合に2つの三角形の頂点が一致する保証がありません。

2019 08 17 14 48 45

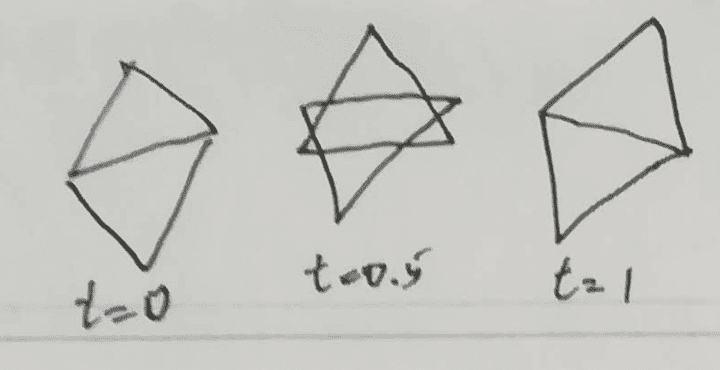
実際にやってみると三角形がばらばらになってしまいます。

三角形のモーフィングを作った。 pic.twitter.com/xZS9k24TU6
— 折登いつき (@MatchaChoco010) May 31, 2019

ここで時刻tでのある理想の頂点をv0, v1, v2, v3とします。

2019 08 17 14 49 18

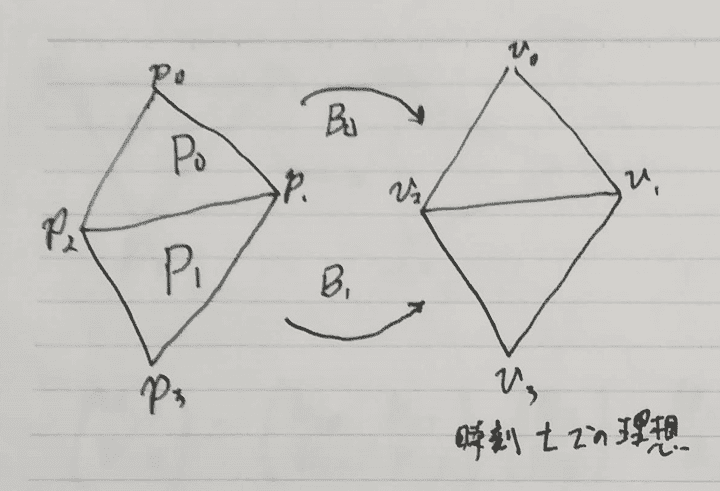
このとき、P0から{v0, v1, v2}への変形は次のように計算できます。

2019 08 17 14 49 34

2019 08 17 14 49 48

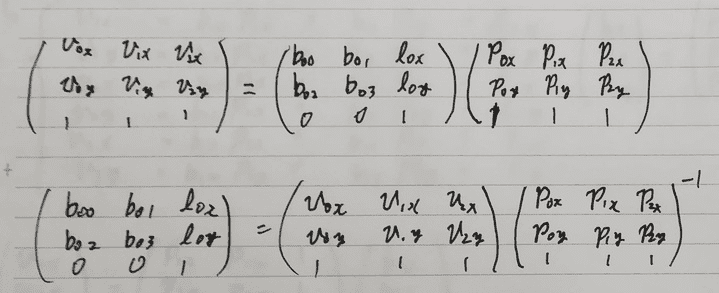
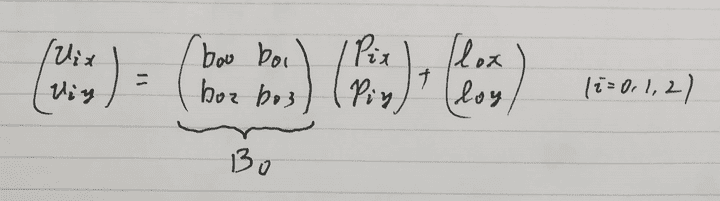
同様にしてP1から{v2, v1, v3}への変形は次のようにして計算できます。

2019 08 17 14 50 01

2019 08 17 14 50 08

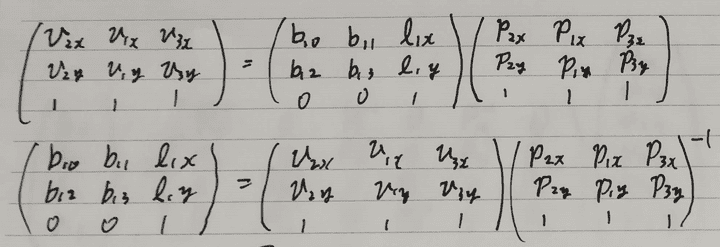
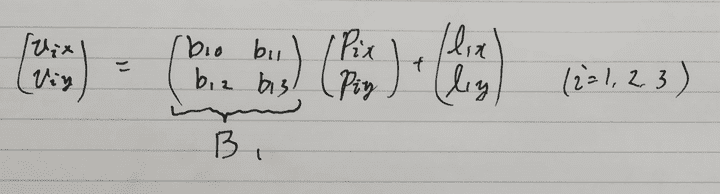
理想の頂点v0, v1, v2, v3のとき、B{0t}とA{0t}は限りなく近く、 B{1t}とA{1t}も限りなく近い変形になっているはずです。つまり、次の式Eを最小にするv0, v1, v2, v3を求めれば、それが時刻tでの頂点の位置ということになります。

2019 08 17 14 50 34

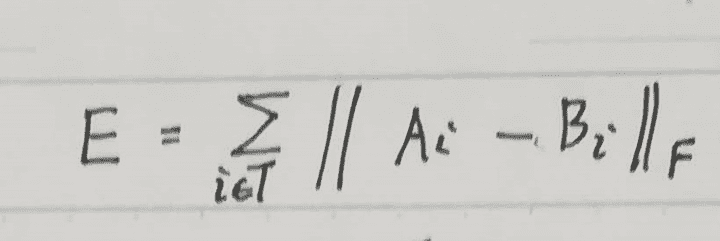
Tは三角形の集合です。

||・||_Fはフロベニウスノルムです。フロベニウスノルムは次のようなものです。

2019 08 17 14 50 52

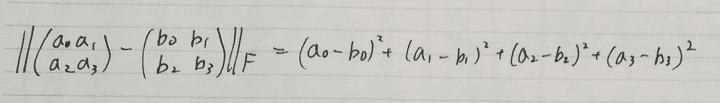
2乗誤差でとても都合がよい形のノルムなのが分かります。

各A{it}についてはPとQの頂点座標から決まります。各B{it}についてはPと{vi}の座標から決まります。 Pの頂点座標とQの頂点座標は既知で、{vi} だけが未知の変数ですね。

ここで、{v0, v1, v2}と{p0, p1, p2}、B_{0t}について次のような計算ができます。

2019 08 17 14 52 53

2019 08 17 14 53 04

2019 08 17 14 53 11

2019 08 17 14 53 19

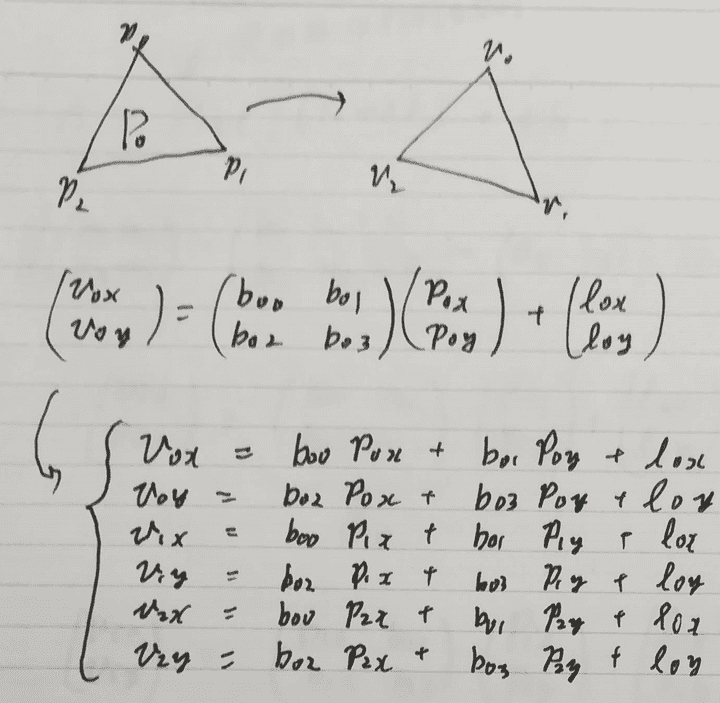
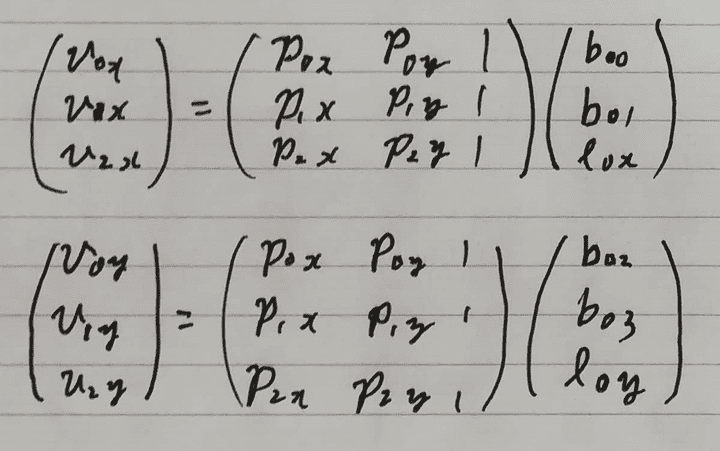
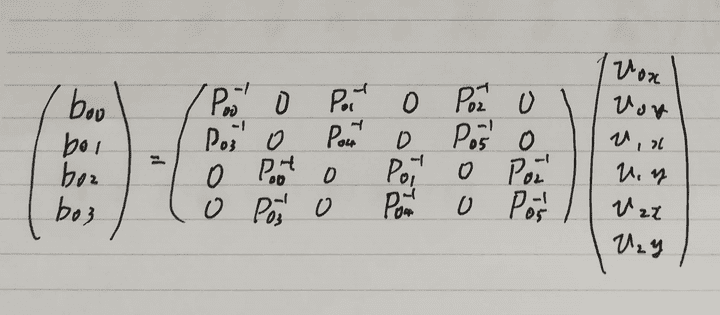
{v2, v1, v3}と{p2, p1, p3}、B_{1t}についても同様の計算ができます。

2019 08 17 14 53 36

2019 08 17 14 53 43

2019 08 17 14 53 54

2019 08 17 14 54 03

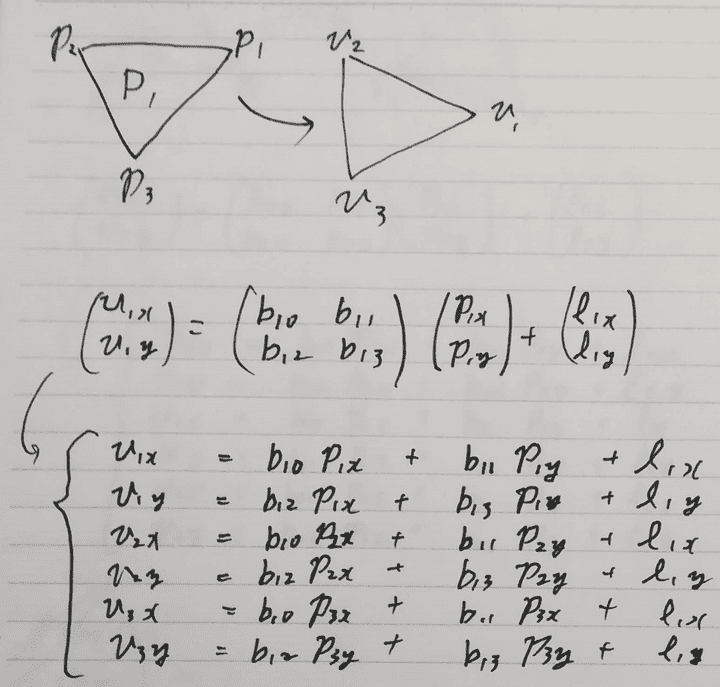
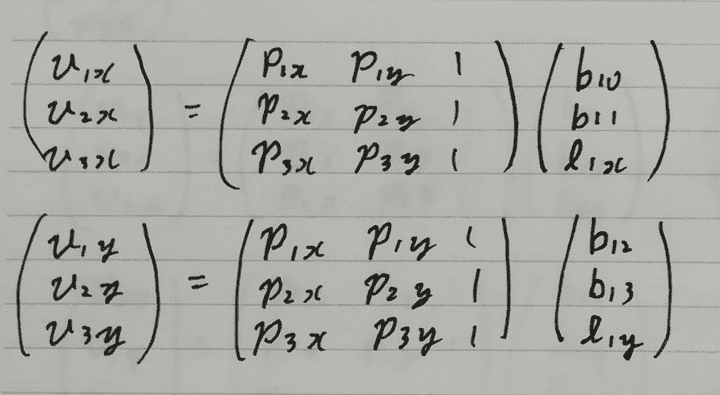
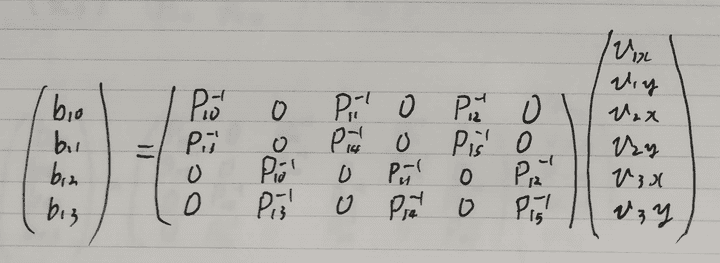
この2つの行列を一つの巨大な行列にまとめることができます。

2019 08 17 14 54 20

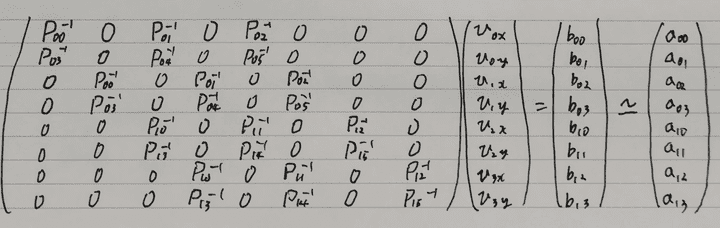
これだけでは回転と拡大縮小成分のみを扱っているので、平行移動成分についても決定するために頂点のコンストレイントを与えます。

0番目の頂点について、v0 = t * qo + (1 - t) * p_0となることを条件に加えます。

2019 08 17 14 54 44

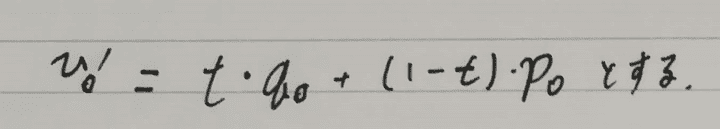
この条件の重みをwとしたときに次のような行列がかけます。コンストレイントとなるポイント数はここでは一つとしていますが必要に応じて適当に追加します。

2019 08 17 14 55 00

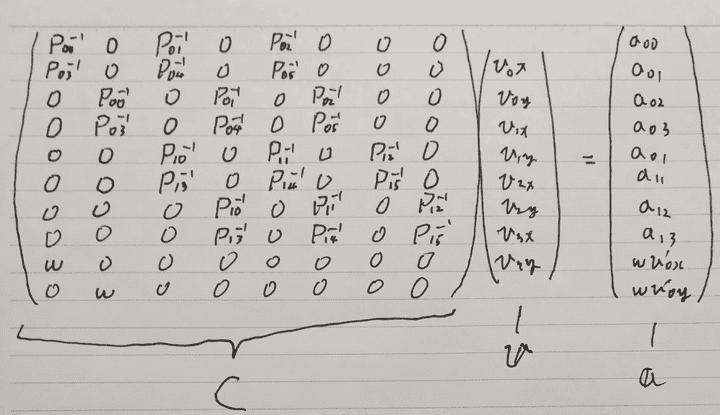
でかい行列をC、右辺をaと置きます。するとCは正方行列ではないので、これは擬似逆行列問題となっています。

2019 08 17 14 55 21

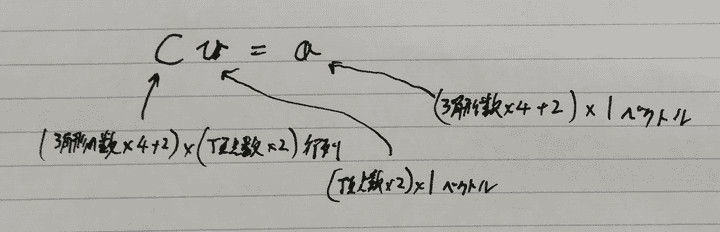
擬似逆行列は2乗誤差を最小にするということでちょうどフロベニウスノルムに対応しています。

両辺にCの転置を左から掛けます。

2019 08 17 14 55 37

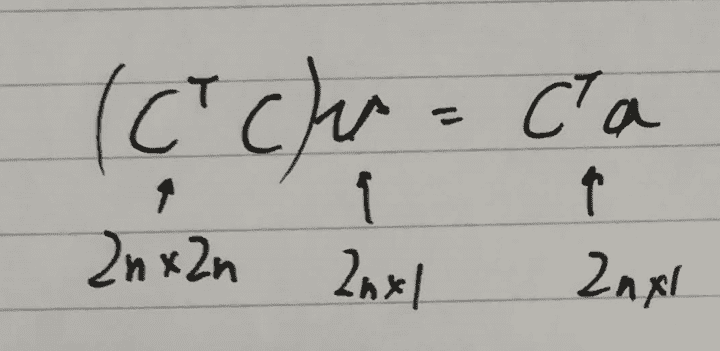
すると普通の逆行列問題になりました。あとはLU分解で線形方程式を解けば無事{v0, v1, v2, v3}の座標が求まります。

頂点数4で三角形数2のときについて書きましたが、頂点数と三角形数が増えても同じことです。 Cはほとんどがゼロで必要なところだけ値が入っている形になります。 $C$ が $(三角形数 \times 4+2 \times コンストレイントの数) \times (2 \times 頂点数)$ 行列となり、 $C^tC$ は $(2 \times 頂点数) \times (2 \times 頂点数)$ 行列となって、 2nx2nの行列の線形方程式をとけば求まるという話になります。

最後にC++で書いたコードを載せておきます。線形代数のライブラリにはEigenを利用しています。 trianglesには三角形の頂点のインデックスが含まれています。 pointsにはPの頂点座標が、editedPointsにはQの頂点座標が渡されるものとしています。

auto arapPoints(const std::vector<Point> &points,
                const std::vector<Point> &editedPoints,
                const std::vector<Triangle> &triangles, const double t) {
  MatrixXd PInverseBlock =
      MatrixXd::Zero(4 * triangles.size() + 2, 2 * points.size());
  VectorXd aVector = VectorXd::Zero(4 * triangles.size() + 2);

  for (unsigned int i = 0; i < triangles.size(); i++) {
    auto triangle = triangles[i];

    Matrix3d p;
    p << points[triangle.p0].x, points[triangle.p1].x, points[triangle.p2].x,
        points[triangle.p0].y, points[triangle.p1].y, points[triangle.p2].y, 1,
        1, 1;
    Matrix3d q;
    q << editedPoints[triangle.p0].x, editedPoints[triangle.p1].x,
        editedPoints[triangle.p2].x, editedPoints[triangle.p0].y,
        editedPoints[triangle.p1].y, editedPoints[triangle.p2].y, 1, 1, 1;

    Matrix3d aff = q * p.inverse();

    Vector2d Translate = aff.block(0, 2, 2, 1);

    Matrix2d A = aff.block(0, 0, 2, 2);

    JacobiSVD<Matrix2d> SVD(A, ComputeFullU | ComputeFullV);

    Matrix2d Ralpha = SVD.matrixU();

    Matrix2d D = SVD.singularValues().asDiagonal();

    Matrix2d Rbeta = SVD.matrixV().transpose();

    Matrix2d Rgamma = Ralpha * Rbeta;

    Matrix2d S = Rbeta.transpose() * D * Rbeta;

    auto theta = atan2(Rgamma(1, 0), Rgamma(0, 0));
    Matrix2d Rtgamma;
    Rtgamma << cos(theta * t), -sin(theta * t), sin(theta * t), cos(theta * t);

    Matrix2d Agammat = Rtgamma * ((1 - t) * Matrix2d::Identity() + t * S);

    Matrix3d afft = Matrix3d::Identity();
    afft.block(0, 0, 2, 2) = Agammat;
    afft.block(0, 2, 2, 1) = Translate * t;

    Matrix3d P;
    P << points[triangle.p0].x, points[triangle.p0].y, 1, points[triangle.p1].x,
        points[triangle.p1].y, 1, points[triangle.p2].x, points[triangle.p2].y,
        1;
    Matrix3d PInverse = P.inverse();

    // b00
    PInverseBlock(4 * i + 0, 2 * triangle.p0 + 0) = PInverse(0, 0);
    PInverseBlock(4 * i + 0, 2 * triangle.p1 + 0) = PInverse(0, 1);
    PInverseBlock(4 * i + 0, 2 * triangle.p2 + 0) = PInverse(0, 2);
    // b01
    PInverseBlock(4 * i + 1, 2 * triangle.p0 + 0) = PInverse(1, 0);
    PInverseBlock(4 * i + 1, 2 * triangle.p1 + 0) = PInverse(1, 1);
    PInverseBlock(4 * i + 1, 2 * triangle.p2 + 0) = PInverse(1, 2);
    // b10
    PInverseBlock(4 * i + 2, 2 * triangle.p0 + 1) = PInverse(0, 0);
    PInverseBlock(4 * i + 2, 2 * triangle.p1 + 1) = PInverse(0, 1);
    PInverseBlock(4 * i + 2, 2 * triangle.p2 + 1) = PInverse(0, 2);
    // b11
    PInverseBlock(4 * i + 3, 2 * triangle.p0 + 1) = PInverse(1, 0);
    PInverseBlock(4 * i + 3, 2 * triangle.p1 + 1) = PInverse(1, 1);
    PInverseBlock(4 * i + 3, 2 * triangle.p2 + 1) = PInverse(1, 2);

    // a00
    aVector(4 * i + 0) = afft(0, 0);
    // a01
    aVector(4 * i + 1) = afft(0, 1);
    // a10
    aVector(4 * i + 2) = afft(1, 0);
    // a11
    aVector(4 * i + 3) = afft(1, 1);
  }

  // point constraint
  double weight = 100;
  PInverseBlock(4 * triangles.size() + 0, 0) = weight;
  PInverseBlock(4 * triangles.size() + 1, 1) = weight;
  aVector(4 * triangles.size() + 0) =
      weight * ((1 - t) * points[0].x + t * editedPoints[0].x);
  aVector(4 * triangles.size() + 1) =
      weight * ((1 - t) * points[0].y + t * editedPoints[0].y);

  // http://www.singularpoint.org/blog/math/eigen-3/
  // partialPivLu <-> fullPivLu
  VectorXd vertexVector = (PInverseBlock.transpose() * PInverseBlock)
                              .partialPivLu()
                              .solve(PInverseBlock.transpose() * aVector);

  std::vector<Point> returnVertices(points.size());
  for (unsigned int i = 0; i < returnVertices.size(); i++) {
    Point p(vertexVector(2 * i), vertexVector(2 * i + 1));
    returnVertices[i] = p;
  }
  return std::move(returnVertices);
}