ガウシアンフィルタとバイラテラルフィルタ

はじめに

CGの基本的な平滑化のフィルタ処理にガウシアンフィルタというものがあります。また、ガウシアンフィルタの重みの付け方を工夫することでエッジ保存する平滑化のフィルタであるバイラテラルフィルタを作成できます。今回は、その両者のフィルタについて軽く調べたので、軽くまとめてみます。

ガウシアンフィルタ

いわゆるガウスぼかしと呼ばれる平滑化フィルタ処理になります。

その名のとおりガウス関数を利用したフィルタ処理になります。具体的には平滑化の重み付けにガウス関数を利用します。

---

最初にガウス関数について軽く紹介をします。1次のガウス関数は次のとおりです。いくつか変種はありますが、基本的にはこのように表現されます。

$G(x) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{x^2}{2\sigma^2}\right)$

2次のガウス関数は次のとおりです。

$G(x, y) = \frac{1}{2\pi\sigma^2}\exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)$

2次のガウス関数は1次のガウス関数をかけ合わせたものになっているという特徴があります。

$G(x, y) = G(x) \cdot G(y)$

3DCGの分野では$\exp$の手前の係数を省略したものもガウス関数と呼ばれることもあるようです。

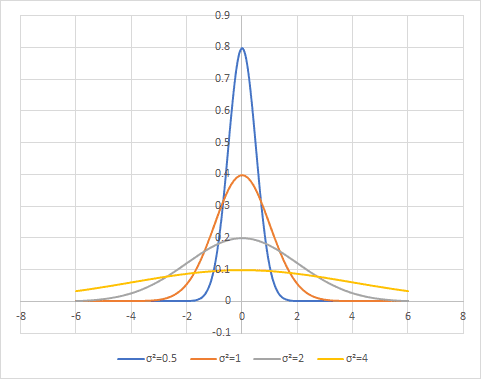
1次のガウス関数をグラフにすると次のようになります。$x = 0$で一番大きな値を取り、$x$が$0$から離れるにつれて小さな値になっていく、釣鐘型の形状となっています。パラメータである$\sigma^2$の大きさを大きくすると山がなだらかになり裾が広くなっていきます。

---

ガウシアンフィルタとは平滑化フィルタの一種です。平滑化フィルタは、あるピクセルに対して周辺のピクセルをブレンドすることで平滑化を行うフィルタのことです。ガウシアンフィルタでは、ぼかすピクセルから遠いピクセルの影響が近いものよりも少なくなるように、ピクセルの影響の重み付けに2次のガウス関数を利用します。

周辺ピクセルの重み付けにガウス関数をそのまま適用するとサンプルする点が$-\infty$から$\infty$までの連続値となりコンピュータの計算には適しません。そこでカーネルという領域で区切り、その中でのみガウス関数に基づく重み付けを行います。ピクセルをブレンドした重みの総和が1になるように、重み付きのピクセルの和を重みで割る必要があります。

カーネルの大きさを5×5にしたときのガウシアンフィルタの式は次のとおりです。

$g(i, j) = \frac{1}{W_1} \sum_{n=-2}^2 \sum_{m=-2}^2 G(n, m) \cdot f(i+n, j+m)$

ただし、$W_1 = \sum_{s=-2}^2 \sum_{t=-2}^2 G(s, t)$とします。

ここで、$f(i, j)$は入力のピクセルの座標$(i, j)$の値を、$g(i, j)$は出力の座標$(i, j)$の値となっています。

周辺ピクセル$(i+n, j+m)$についてガウス関数に基づいた重みをつけて足し合わせています。そのままでは重みを乗じた分だけ大きくなりすぎるので、重みで割ることにより帳尻を合わせています。

---

図を利用して説明すると次のような感じです。

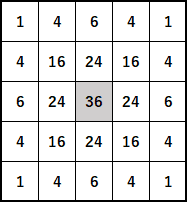
次の図はカーネルのイメージ図です。

5×5のマス目の中心がレンダリング対象のピクセルで、その周辺のマス目がレンダリングに影響するピクセルになります。

このマス目に書かれた数字は実際にはガウス関数の値を利用します。マス目に書かれた数字をピクセルの値に乗じて足し合わせることで中心のピクセルほど重みのついた加重和となります。このままでは乗じた分だけ値が大きくなりすぎてしまうので、重みの総和が1になるように重みの総計で割ります。この場合は各マスの重みの総計である256で割って正規化を行います。

ガウシアンフィルタでは、カーネルのサイズとガウス関数のパラメータである$\sigma^2$の値を変えることでフィルタのかかり具合を変えることができます。カーネルを大きくすると広い範囲が影響するようになるためぼかし具合が大きくなりますが、その分テクスチャの参照数が増え負荷が増すため処理が重たくなります。$\sigma^2$の値を小さくするとすぐ近くのピクセル以外は影響しなくなるのでぼかし幅が小さくなり、大きくすると距離による影響力の低下幅が小さくなるため大きくぼかされます。

ぼかしを大きくしたい場合はカーネルの大きさをいじるよりも、複数回フィルタ処理をかけたほうが負荷が少なく済むようです。

---

このガウシアンフィルタを単純に実装すると1ピクセルあたり25回のテクスチャの参照が必要になります。しかし、$G(x, y) = G(x) \cdot G(y)$の関係を利用しフィルタ処理を2パスで計算することによりテクスチャの参照数を減らすことができます。

$g(i, j) = \frac{1}{W_2} \sum_{n=-2}^2 G(n) \cdot \frac{1}{W_2} \sum_{m=-2}^2 G(m) \cdot f(i+n, j+m)$

ただし、$W_2 = \sum_{s=-2}^2 G(s)$とします。

---

このガウシアンフィルタをcanvasで実装したデモがこちらになります。

このデモを実行した結果は次のようになります。

大きくぼかしたいときはカーネルを大きくするよりも、複数回フィルタをかけたほうが高速に同様の結果を得ることができます。

バイラテラルフィルタ

バイラテラルフィルタはエッジ保存平滑化フィルタの一種です。ガウシアンフィルタがベースのフィルタです。ガウシアンフィルタでは画面全体を一様にぼかしていました。バイラテラルフィルタでは画像のエッジとなる部分を残しながらぼかしていきます。

---

バイラテラルフィルタでは、中心と大きさの大きく違うピクセルの影響力を小さくすることでエッジとなっている部分を保存します。今回は各ピクセルの大きさとして輝度を用います。$l(x)$を$x$の輝度を求める関数とします。

カーネルの大きさを5×5にしたときのバイラテラルフィルタの式は次のとおりです。

$g(i, j) = \frac{1}{W_3} \sum_{n=-2}^2 \sum_{m=-2}^2 G(n, m) \cdot G(l(f(i, j)) - l(f(i+n, j+m))) \cdot f(i+n, j+m)$

ただし、$W_3 = \sum_{s=-2}^2 \sum_{t=-2}^2 G(s, t) \cdot G(l(f(i, j)) - l(f(i+s, j+t)))$とします。

さきほどのガウシアンフィルタの式の重みの部分に、ピクセルの輝度の差をもとにした1次のガウス関数がかかっています。

---

図を使って説明をしていきます。

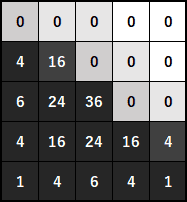
次の図はバイラテラルフィルタのカーネルのイメージ図です。

さきほどのガウシアンフィルタと比べてみると、中心のピクセルと輝度の大きく違うところは影響力が0になっています。実際には影響度は0か1かの判定ではなくて、輝度の大きさの差に応じたガウス関数を利用します。

このようにすることで輝度が似ている範囲だけでぼかされ、輝度の大きく異なっているエッジの部分はぼかしに影響しにくくなり、エッジの残ったぼかしを行うことができます。このようにしてバイラテラルフィルタではエッジを保存した平滑化を行っています。

ガウシアンフィルタではパラメータとなる$\sigma^2$は1つだけでしたが、バイラテラルフィルタではガウス関数が2つ使われているためパラメータが2つになります。一方はぼかしの周辺ピクセルの影響力を決めるガウス関数のパラメータ$\sigma_1^2$で、もう一方はエッジの判定の輝度の差に対してかかるガウス関数のパラメータ$\sigma_2^2$です。2つのパラメータを利用するためバイラテラルフィルタという名前なようです。

---

このバイラテラルフィルタをcanvasで実装したデモがこちらになります。

このデモを実行した結果は次のようになります。

複数回適用すると細かいテクスチャが消え、絵画のような面白い結果になります。

おわりに

さまざまなフィルタ処理の基本となるガウシアンフィルタと、その応用のひとつであるバイラテラルフィルタについてまとめました。これらのフィルタは3DCGでも頻繁に使われるもののようなのでしっかりとおさえておきたいです。