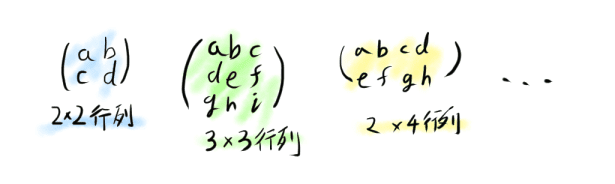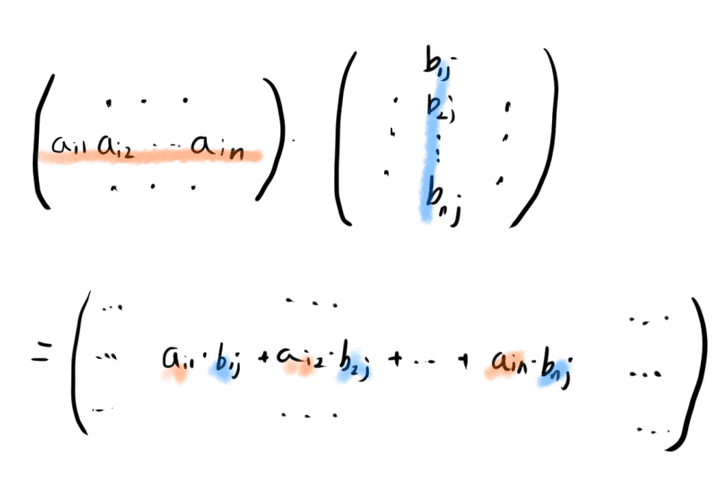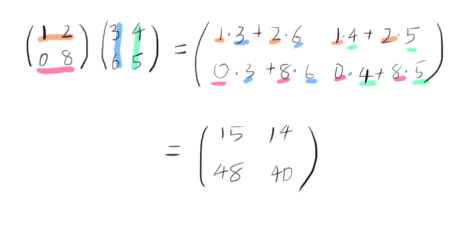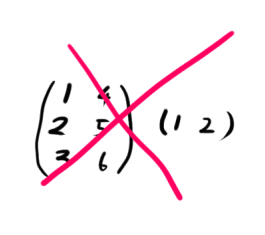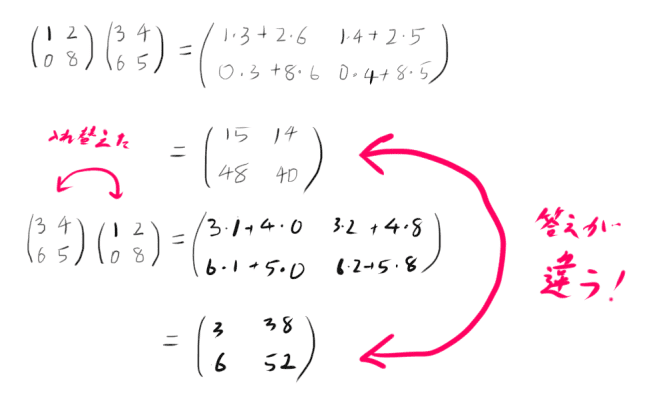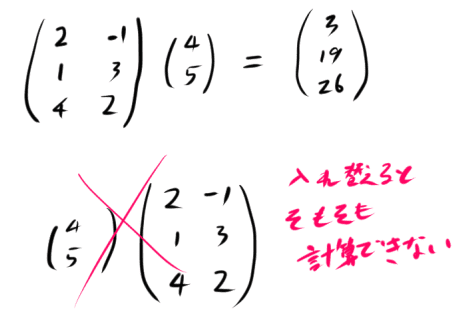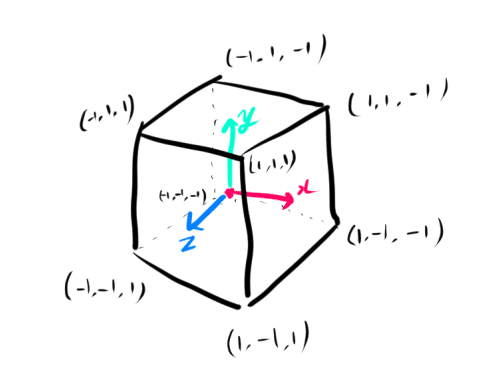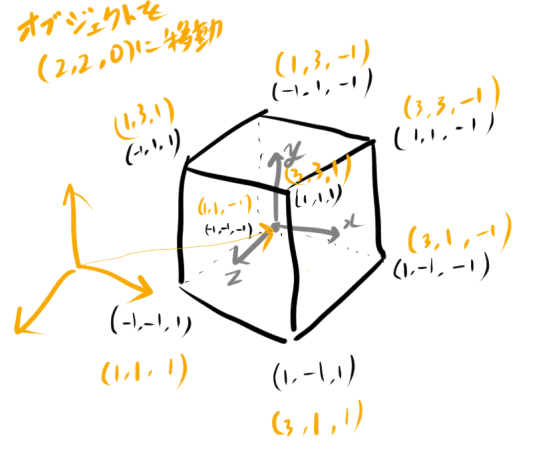MVP行列による座標変換について

はじめに

前回の記事で頂点シェーダでの座標変換の話が出てきました。 多くの場合、頂点シェーダでは入力の頂点座標にMVP行列を掛ける作業を行います。 今回の記事では、このMVP行列についてざっくり解説を行います。

まず最初に行列の導入と行列による座標変換を紹介します。 その後、Model行列、View行列、Projection行列の順で説明していきます。

行列の導入

行列とは数字を縦横に並べたものです。 縦に$m$個、横に$n$個ならべたものを$m×n$行列と呼びます。

$\left( \begin{array}{cc} a & b \\ c & d \end{array} \right), \left( \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \right), \left( \begin{array}{ccc} a & b & c \\ d & e & f \end{array} \right), \left( \begin{array}{cc} a & b \\ c & d \\ e & f \\ g & h \end{array} \right), \left( \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array} \right)$

左から順に、$2×2$行列、$3×3$行列、$2×3$行列、$4×2$行列、$m×n$行列です。

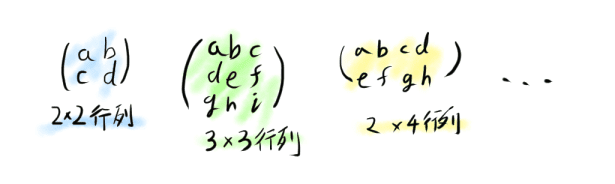
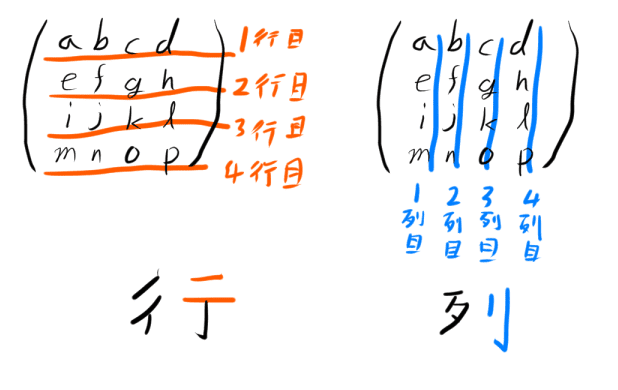
それぞれの行を1行目2行目...と数え、 それぞれの列を1列目2列目...と数えます。

行列の掛け算

$l×m$行列と$m×n$行列の積は次のように定義されます。

$\left( \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1m} \\ a_{21} & a_{22} & \ldots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{l1} & a_{l2} & \ldots & a_{lm} \end{array} \right) \left( \begin{array}{cccc} b_{11} & b_{12} & \ldots & b_{1n} \\ b_{21} & b_{22} & \ldots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \ldots & b_{mn} \end{array} \right) = \left( \begin{array}{cccc} \displaystyle\sum_{j=1}^{m}a_{1j}b_{j1} & \displaystyle\sum_{j=1}^{m}a_{1j}b_{j2} & \ldots & \displaystyle\sum_{j=1}^{m}a_{1j}b_{jn} \\ \displaystyle\sum_{j=1}^{m}a_{2j}b_{j1} & \displaystyle\sum_{j=1}^{m}a_{2j}b_{j2} & \ldots & \displaystyle\sum_{j=1}^{m}a_{2j}b_{jn} \\ \vdots & \vdots & \ddots & \vdots \\ \displaystyle\sum_{j=1}^{m}a_{lj}b_{j1} & \displaystyle\sum_{j=1}^{m}a_{lj}b_{j2} & \ldots & \displaystyle\sum_{j=1}^{m}a_{lj}b_{jn} \end{array} \right)$

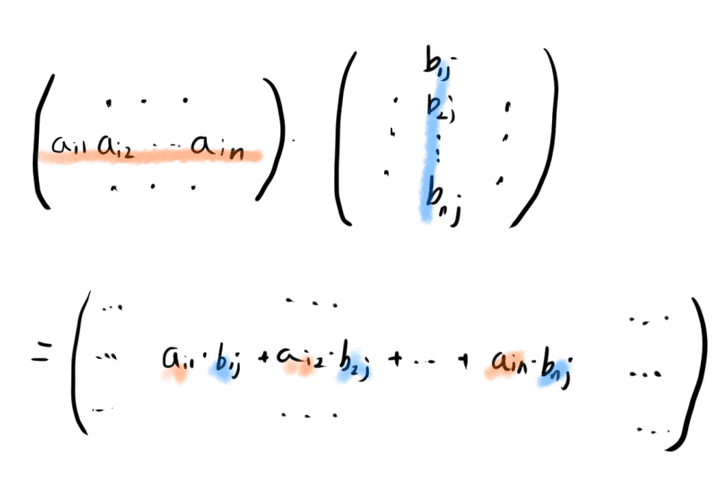
行列同士の掛け算の例をいくつか出してみます。

$\left( \begin{array}{rrr} 4 & -2 & 2 \\ \end{array} \right) \left( \begin{array}{r} 5 \\ 3 \\ 1 \\ \end{array} \right) = 4\cdot5+(-2)\cdot3+2\cdot1 = 16$ $\left( \begin{array}{rr} 2 & -1 \\ 1 & 3 \\ 4 & 2 \end{array} \right) \left( \begin{array}{r} 4 \\ 5 \end{array} \right) = \left( \begin{array}{c} 2\cdot4+(-1)\cdot5 \\ 1\cdot4+3\cdot5 \\ 4\cdot4+2\cdot5 \end{array} \right) = \left( \begin{array}{ccc} 3 \\ 19 \\ 26 \end{array} \right)$ $\left( \begin{array}{cc} 1 & 2 \\ 0 & 8 \end{array} \right) \left( \begin{array}{cc} 3 & 4 \\ 6 & 5 \end{array} \right) = \left( \begin{array}{cc} 1\cdot3+2\cdot6 & 1\cdot4+2\cdot5 \\ 0\cdot3+8\cdot6 & 0\cdot4+8\cdot5 \end{array} \right) = \left( \begin{array}{cc} 15 & 14 \\ 48 & 40 \end{array} \right)$ $\left( \begin{array}{cc} 3 & 4 \\ 6 & 5 \end{array} \right) \left( \begin{array}{cc} 1 & 2 \\ 0 & 8 \end{array} \right) = \left( \begin{array}{cc} 3\cdot1+4\cdot0 & 3\cdot2+4\cdot8 \\ 6\cdot1+5\cdot0 & 6\cdot2+5\cdot8 \end{array} \right) = \left( \begin{array}{cc} 3 & 38 \\ 6 & 52 \end{array} \right)$

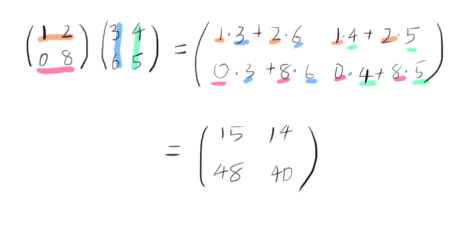
１つ目の行列の列数と2つ目の行列の行数が等しくないと掛け算はできません。

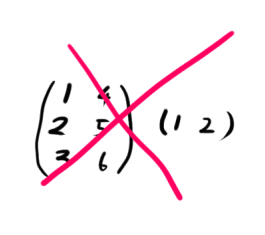
行列の掛け算は前後の順番を入れ替えられません。

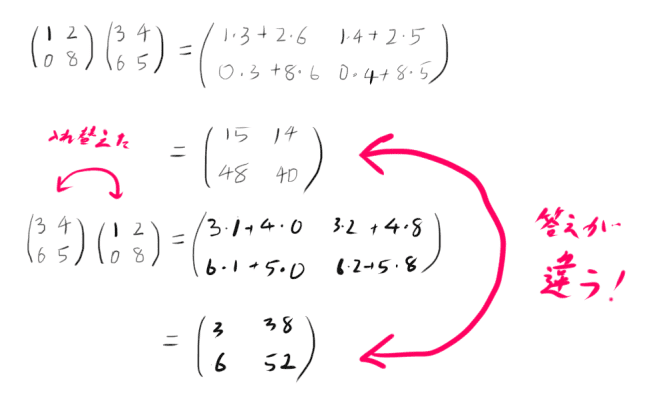
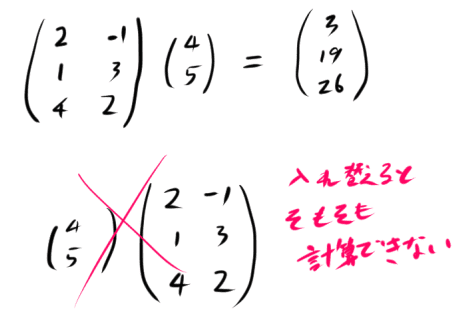
行列の積には結合法則が成り立ちます。 行列$A, B, C$の積$ABC$について、 前から先に計算しても後ろから先に計算しても等しくなります。

$(AB)C = A(BC)$

---

他にも足し算やスカラー倍、転置をとったり逆行列をとったりと、 行列にはさまざまな計算がありますが、今回は使わないので説明は省略します。

行列と連立方程式

行列の導入と掛け算について説明をしました。 行列は数字が複数組み合わさったものなので掛け算の計算も複雑です。 なぜあのように面倒な計算なのでしょうか。

分数の足し算は「通分をしてから分子だけを足す」というルールが有りましたが、 このルールにはきちんとした意味があるものでした。 たとえば$\frac{1}{2}$と$\frac{1}{3}$を足す場合、 ケーキのホールの半分と$\frac{1}{3}$を考えてみると 6等分を単位として考える意味がわかります。

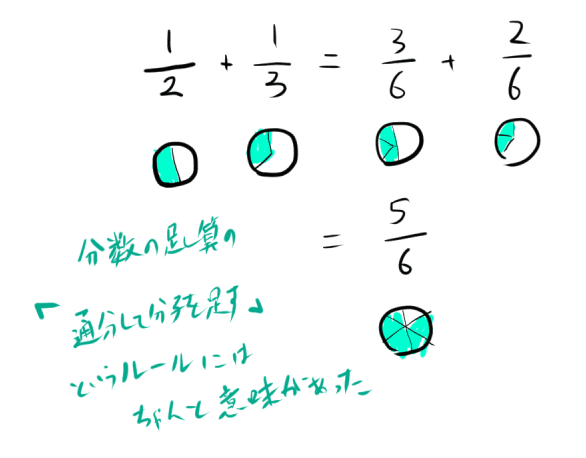
行列のよくわからない計算のルールにも、このような意味があるのでしょうか。

行列の計算の意味といってもいろいろとありますが、 ここでは「連立方程式の便利表記」という意味を説明していきます。

---

次のような連立方程式の問題を解く場合を考えてみましょう。

プリンを3個とヨーグルトを2個買ったら690円でした。 プリンを4個とヨーグルトを5個買ったら1200円でした。 プリンとヨーグルトはそれぞれ何円でしょう。

まずは行列を使わずに普通に解いてみましょう。 プリンの値段を$x$円、ヨーグルトの値段を$y$円とします。 すると次のような式がたてられます。

$\begin{cases} 690 = 3x + 2y & \\ 1200 = 4x + 5y & \end{cases}$

あとはこの連立方程式を解けばよいだけですね。

この連立方程式は行列で表記できます。

$\left( \begin{array}{c} 690 \\ 1200 \end{array} \right) = \left( \begin{array}{cc} 3 & 2 \\ 4 & 5 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$

この例だけでは行列表記したところであまりありがたみが感じられませんね。

もうひとつ例題を出してみます。

プリンを1個とヨーグルトを2個のセットAがあります。 プリンを2個とヨーグルトを3個のセットBがあります。 セットAを2個とセットBを1個買ったら960円でした。 セットAを2個とセットBを2個買ったら1400円でした。 プリンとヨーグルトはそれぞれ何円でしょう。 セットの値段に割引はないものとします。

今回は連立方程式を二段階に立てる必要があります。 プリンの値段を$x$円、ヨーグルトの値段を$y$円とします。 セットAの値段を$x'$円、セットBの値段を$y'$円とします。 すると次のような式がたてられます。

$\begin{cases} x' = 1x + 2y & \\ y' = 2x + 3y & \end{cases}$ $\begin{cases} 960 = 2x' + 1y' & \\ 1400 = 2x' + 2y' & \end{cases}$

これを行列を使って表記してみましょう。

$\left( \begin{array}{c} x' \\ y' \end{array} \right) = \left( \begin{array}{cc} 1 & 2 \\ 2 & 3 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$ $\left( \begin{array}{c} 960 \\ 1400 \end{array} \right) = \left( \begin{array}{cc} 2 & 1 \\ 2 & 2 \end{array} \right) \left( \begin{array}{c} x' \\ y' \end{array} \right)$

1つ目の式の$\left( \begin{array}{c} x' \\ y' \end{array} \right)$を2つ目の式に代入してみましょう。

$\left( \begin{array}{c} 960 \\ 1400 \end{array} \right) = \left( \begin{array}{cc} 2 & 1 \\ 2 & 2 \end{array} \right) \Bigg( \left( \begin{array}{cc} 1 & 2 \\ 2 & 3 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) \Bigg)$

結合法則が成り立つので前の行列の積の部分から掛け算ができますね。

$\begin{aligned} \left( \begin{array}{c} 960 \\ 1400 \end{array} \right) & = \left( \begin{array}{cc} 2 & 1 \\ 2 & 2 \end{array} \right) \left( \begin{array}{cc} 1 & 2 \\ 2 & 3 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)\\ & = \left( \begin{array}{cc} 2\cdot1+1\cdot2 & 2\cdot2+1\cdot3 \\ 2\cdot2+1\cdot2 & 2\cdot2+2\cdot3 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)\\ & = \left( \begin{array}{cc} 4 & 7 \\ 6 & 10 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) \end{aligned}$

二段階の連立方程式が2個の行列の積で簡潔に表記できました。 これが行列の掛け算の強みです。

今回はまだ2段階でしたが、3段階4段階と連立方程式が連なっていく場合、 行列で表記したほうが簡潔でわかりやすい表記ができます。 連立方程式がそんなに何個も連なることは滅多にないだろうと思われるかもしれませんが、 3DCGを扱っていると頻繁にでてきます。 それについてはこれからの説明で分かると思います。

---

行列の利点として、行列の計算はGPUで高速に行えるというのもあります。 行列はGPU上で大量の頂点の座標変換を行うのに適した形ということですね。 計算の仕方がややこしくて覚えられない人も気にすることはありません。 計算は全部コンピュータがやってくれます。

行列と座標変換

行列の計算についてはいったんおいて3DCGのモデルについて説明をします。

モデルの頂点座標はモデルの原点からの相対座標で保持されています。 このモデルの原点からの相対座標のことをローカル座標と呼ぶことがあります。

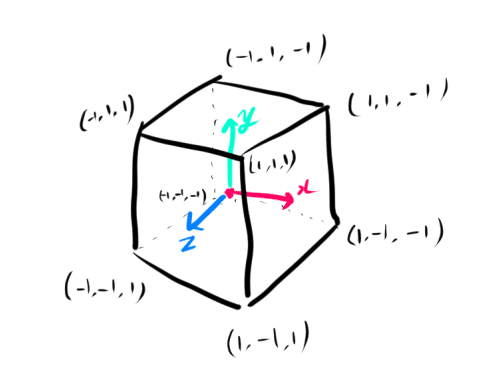
Unityなどでモデルを特定の座標に配置したり拡大縮小や回転などを行うことがあります。

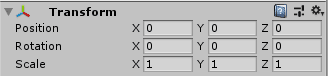
上の立方体のモデルを特定の座標に配置したり拡大縮小や回転を行う場合を 考えてみましょう。

立方体のモデルを$(2, 2, 0)$の位置に配置した場合、 各頂点の座標は$(2, 2, 0)$だけ足されたものになります。

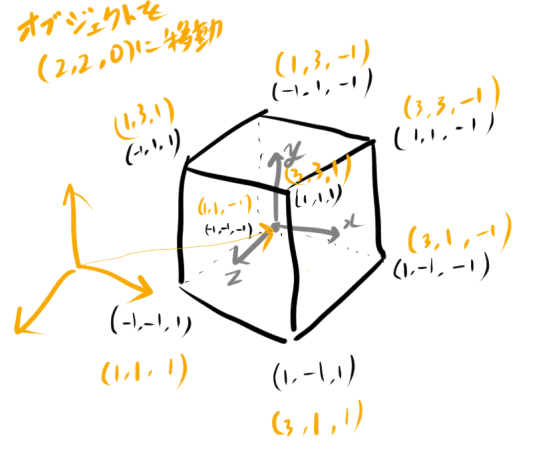
この配置したあとの座標をワールド座標とよんだりグローバル座標と呼んだりします。

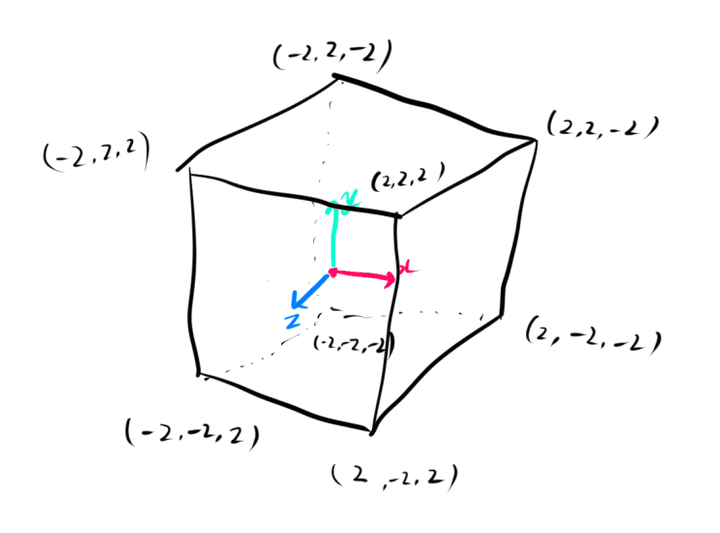
立方体のモデルを2倍に拡大した場合、 各頂点のローカル座標を2倍したものになります。

立方体のモデルをy軸中心に45度回転した場合、 次の図のようになります。

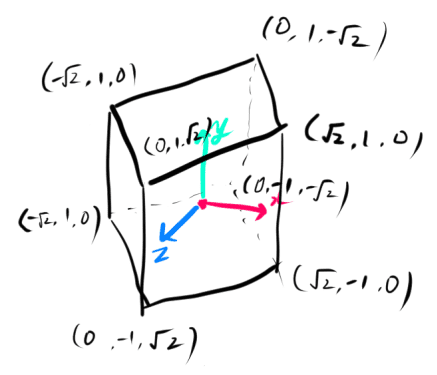
立方体を1/2倍して$(2, 2, 0)$に設置した場合は 次の図のようになります。

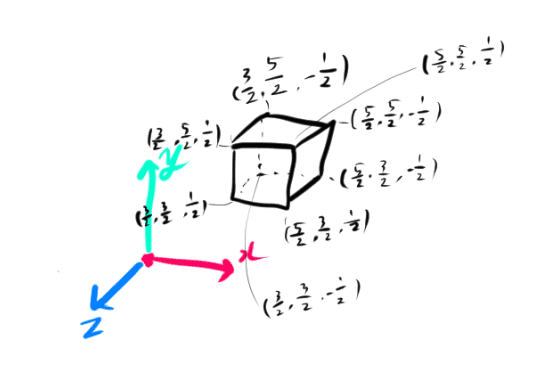
これらの例のようなモデルの平行移動と回転、拡大縮小を行うものを モデル変換と呼びます。 ローカル座標とをモデル変換することでワールド座標に変換されます。

---

これらの座標変換は行列で簡単に表せます。

説明を簡単にするために2次元で説明をしていきます。

今回は次の正方形のモデルを使って説明していきます。

---

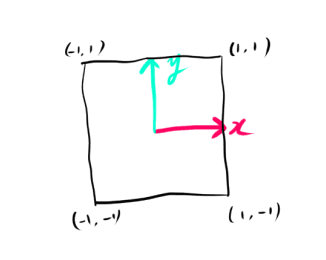
まず最初に拡大縮小について考えてみましょう。

正方形のモデルを原点中心に2倍に拡大することを考えてみます。

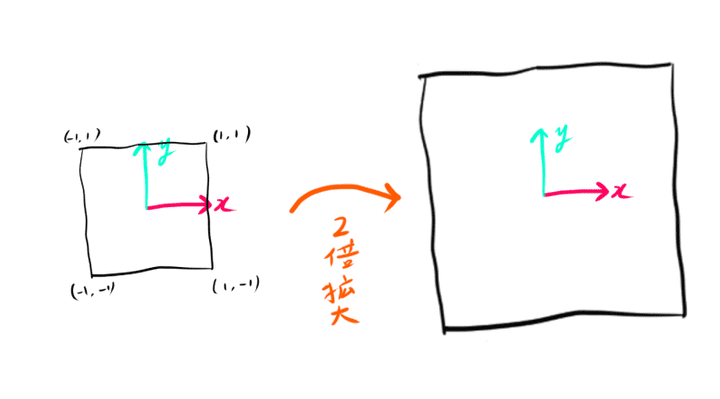
モデルのローカル座標$(x, y)$を2倍拡大する変換によって$(x', y')$に変換したとすると、 次のような連立方程式がたてられます。

$\begin{cases} x' = 2x & \\ y' = 2y & \end{cases}$

すべての頂点がきちんとこの連立方程式のとおりになっていることが分かります。

この連立方程式を行列に直すと次のようになります。

$\left( \begin{array}{c} x' \\ y' \end{array} \right) = \left( \begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$

次に正方形のモデルを原点中心に$x$方向に$2$倍、 $y$方向に$\frac{1}{2}$倍することを考えてみます。

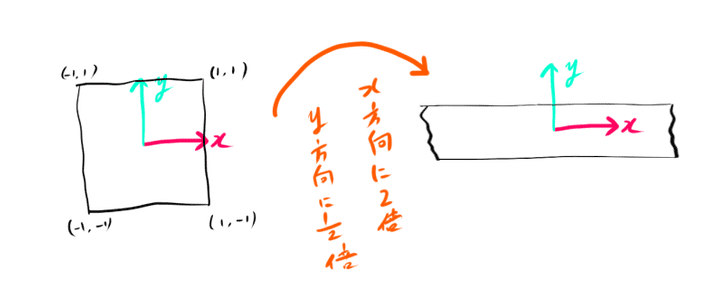
モデルのローカル座標$(x, y)$を$x$方向に$2$倍、$y$方向に$\frac{1}{2}$拡大する変換によって $(x', y')$に変換したとすると、次のような連立方程式がたてられます。

$\begin{cases} x' = 2x & \\ y' = \frac{1}{2}y & \end{cases}$

この連立方程式を行列に直すと次のようになります。

$\left( \begin{array}{c} x' \\ y' \end{array} \right) = \left( \begin{array}{cc} 2 & 0 \\ 0 & \frac{1}{2} \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$

一般に原点中心に$x$方向に$S_x$倍、$y$方向に$S_y$倍する拡大縮小は次のように表現できます。

$\left( \begin{array}{c} x' \\ y' \end{array} \right) = \left( \begin{array}{cc} S_x & 0 \\ 0 & S_y \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$

---

次に原点中心の回転について考えます。

正方形のモデルを30度回転した場合を考えてみます。

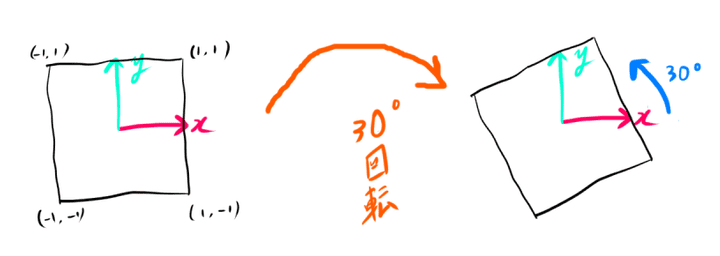
次の図で$OP=r$とします。

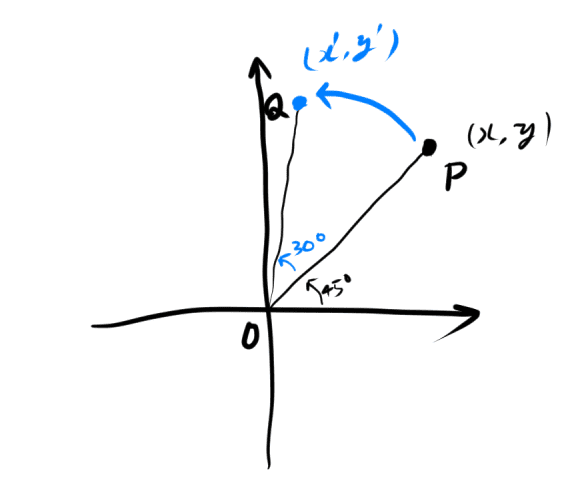
$OP$と$x$軸のなす角が$\frac{\pi}{4}$なので次の式がたてられます。

$x=r\cos(\frac{\pi}{4}), y=r\sin(\frac{\pi}{4})$

また$OQ$から次の式が得られます。

$\begin{cases} x'=r\cos(\frac{\pi}{4}+\frac{\pi}{6}) & \\ y'=r\sin(\frac{\pi}{4}+\frac{\pi}{6}) & \end{cases}$

加法定理を利用すると次のように変形できます。

$\begin{cases} x'=r(\cos(\frac{\pi}{4})\cos(\frac{\pi}{6})-\sin(\frac{\pi}{4})\sin(\frac{\pi}{6})) & \\ y'=r(\sin(\frac{\pi}{4})\cos(\frac{\pi}{6})+\cos(\frac{\pi}{4})\sin(\frac{\pi}{6})) & \end{cases}$

ここに$x=r\cos(\frac{\pi}{4}), y=r\sin(\frac{\pi}{4})$を代入すると 連立方程式はこのようになります。

$\begin{cases} x' = \cos(\frac{\pi}{6})x - \sin(\frac{\pi}{6})y & \\ y' = \sin(\frac{\pi}{6})x + \cos(\frac{\pi}{6})y & \end{cases}$

この連立方程式を行列に直すと次のようになります。

$\left( \begin{array}{c} x' \\ y' \end{array} \right) = \left( \begin{array}{cc} \cos(\frac{\pi}{6}) & -\sin(\frac{\pi}{6}) \\ \sin(\frac{\pi}{6}) & \cos(\frac{\pi}{6}) \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$

一般に$\theta$だけ回転する変換を考えてみます。

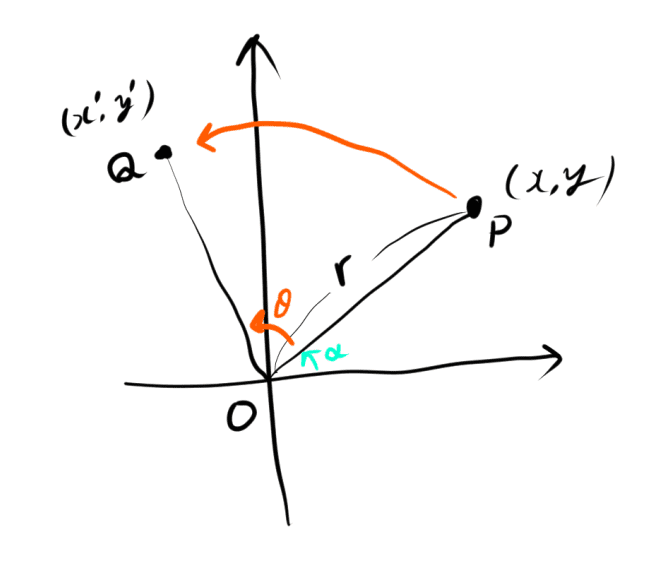
$OP$と$x$軸のなす角を$\alpha$とします。 すると次の式がたてられます。

$x=r\cos\alpha, y=r\sin\alpha$

また$OQ$から次の式が得られます。

$\begin{cases} x'=r\cos(\alpha+\theta) & \\ y'=r\sin(\alpha+\theta) & \end{cases}$

加法定理を利用すると次のように変形できます。

$\begin{cases} x'=r(\cos\alpha\cos\theta-\sin\alpha\sin\theta) & \\ y'=r(\sin\alpha\cos\theta+\cos\alpha\sin\theta) & \end{cases}$

ここに$x=r\cos\alpha, y=r\sin\alpha$を代入すると 連立方程式はこのようになります。

$\begin{cases} x' = x\cos\theta - y\sin\theta & \\ y' = x\sin\theta + y\cos\theta & \end{cases}$

これを行列になおすと次のようになります。

$\left( \begin{array}{c} x' \\ y' \end{array} \right) = \left( \begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right)$

---

最後に平行移動について考えてみます。 これはちょっと曲者です。

正方形のモデルをx方向に1、y方向に2動かした場合を考えてみましょう。

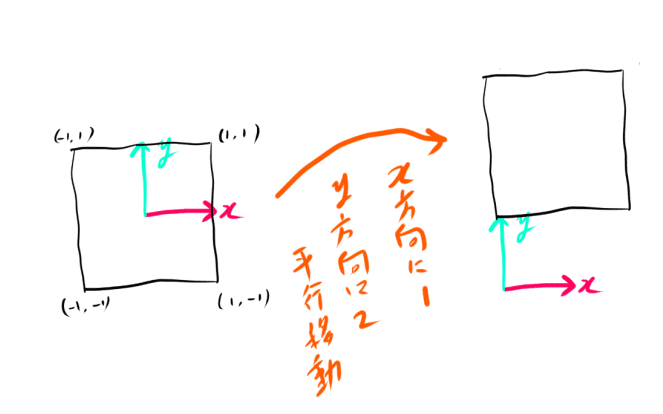
この場合の連立方程式は次のようになります。

$\begin{cases} x' = x + 1 & \\ y' = y + 2 & \end{cases}$

この連立方程式は、2×2の行列では表現できません。

そこで同次座標というのを導入します。 同次座標というのは大雑把にいうと要素を一個足したベクトルです。 $(1, 2)$は$(1, 2, 1)$の様に最後に1を足して表現します。 同次座標はひとつの座標に対して複数の表現があります。 $(1, 2, 1)$と$(2, 4, 2)$、$(3, 6, 3)$などはすべて等しい座標を表現しています。 ちょうど分数と同じですね。 $\frac{1}{2}$は$\frac{2}{4}$、$\frac{3}{6}$も同じものであるのと同様です。 最後の付け加えた要素が分数の分母にあたるものとなっています。 通常は1を付け加えます。

同次座標を使ってこの平行移動を表すと次のようになります。

$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

一般に$x$方向に$T_x$、$y$方向に$T_y$だけ平行移動する場合、次のような行列で表現できます。

$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

---

拡大縮小と回転についても同次座標系に拡張してみます。

拡大縮小は次のとおり。

$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

回転は次のとおりです。

$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

左上の2×2成分がそのまんまですね。

---

複数の要素を組み合わせたモデル変換について考えてみましょう。 ここらへんから行列の威力が発揮されてきます。

2倍拡大してx方向に2、y方向に2平行移動する変換を考えてみます。

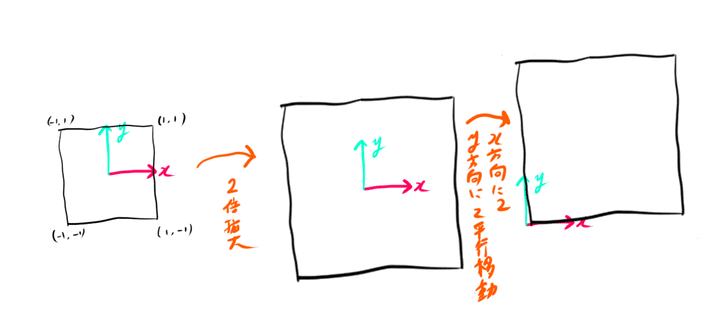
$(x, y)$を2倍に拡大して$(x',y')$に写し、 その$(x', y')$を平行移動して$(x'',y'')$に写したものと考えます。

まず最初に2倍に拡大するのは次のような式で表現できます。

$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

次に平行移動については次のように表現できますね。

$\left( \begin{array}{c} x'' \\ y'' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)$

この２つの式をまとめると次のようになります。

$\left( \begin{array}{c} x'' \\ y'' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 2 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

この式で2倍拡大してから平行移動している式になっています。

拡大縮小が原点中心なので、拡大縮小をしてから平行移動していることに注意です。 順番を逆にすることはできません。

行列の掛け算で変換を順番に行っていくのがそのまま式に表現できますね。

次に$\frac{1}{2}$倍拡大し、$30$度回転して$x$方向に$2$、 $y$方向に$-2$平行移動する変換を考えてみます。

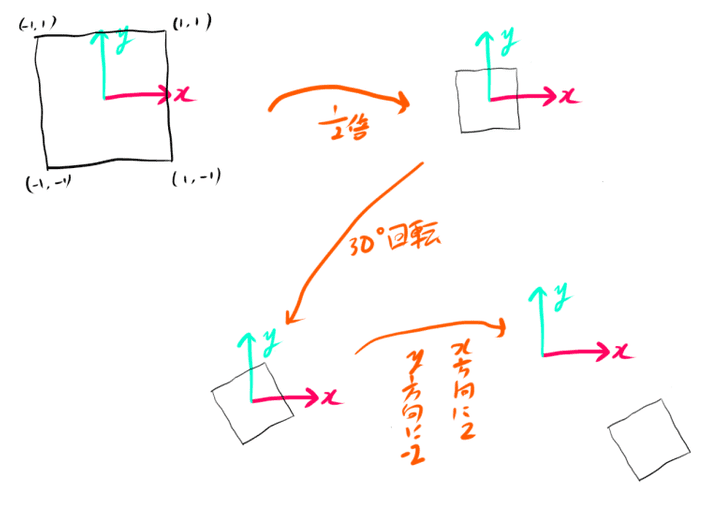
これも行列の積を使えば次のような式で表せます。

$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 2 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} \cos\frac{\pi}{6} & -\sin\frac{\pi}{6} & 0 \\ \sin\frac{\pi}{6} & \cos\frac{\pi}{6} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$

行列の積で連立方程式を表現する強みがわかってきたのではないでしょうか。

行列の計算自体はプログラムでコンピュータに任せられます。 面倒な計算自体はしなくても最初の式さえたてられれば問題ありません。 そう考えるととても便利なことが分かるでしょう。

次にもっと複雑な例で斜め45度方向に拡大する変換を考えてみます。

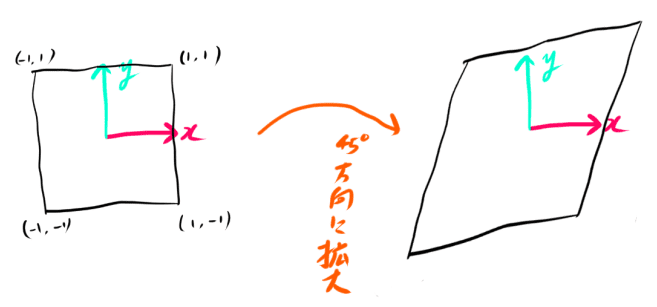
単純な拡大縮小ではx方向かy方向にしか拡大できません。 この場合はいったん逆方向に45度回転してからx方向に拡大し、その後45度回転してもとに戻します。

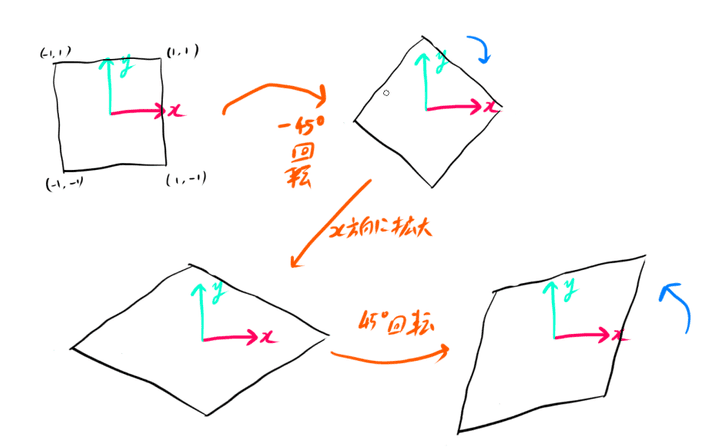
式にすると次のとおりです。

$\begin{aligned} \left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) =& \left( \begin{array}{ccc} \cos\frac{\pi}{4} & -\sin\frac{\pi}{4} & 0 \\ \sin\frac{\pi}{4} & \cos\frac{\pi}{4} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} S_x & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)\\ &\;\;\;\;\; \left( \begin{array}{ccc} \cos(-\frac{\pi}{4}) & -\sin(-\frac{\pi}{4}) & 0 \\ \sin(-\frac{\pi}{4}) & \cos(-\frac{\pi}{4}) & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right) \end{aligned}$

行列を使わないと複雑な連立方程式になるものが、 簡単に掛け算を重ねていくことで作れるのは面白くなってきませんか？

もう一つ、例を上げておきましょう。

正方形を$(1, 1)$中心に2倍拡大し回転する変換について考えます。

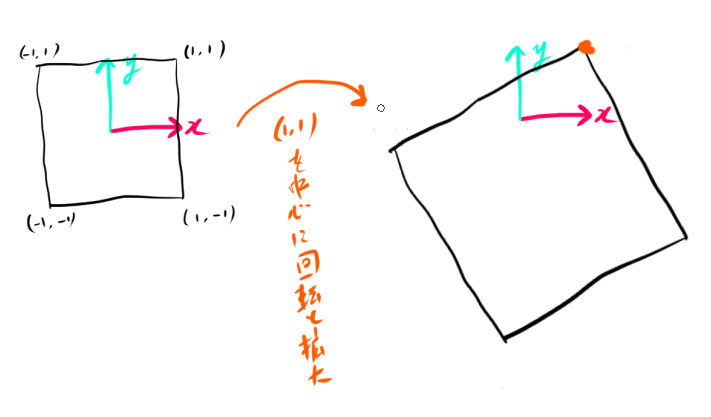
回転も拡大も原点中心にしか行なえません。 この場合はいったん平行移動して原点中心にしてから拡大と回転を行い、 その後平行移動でもとに戻します。

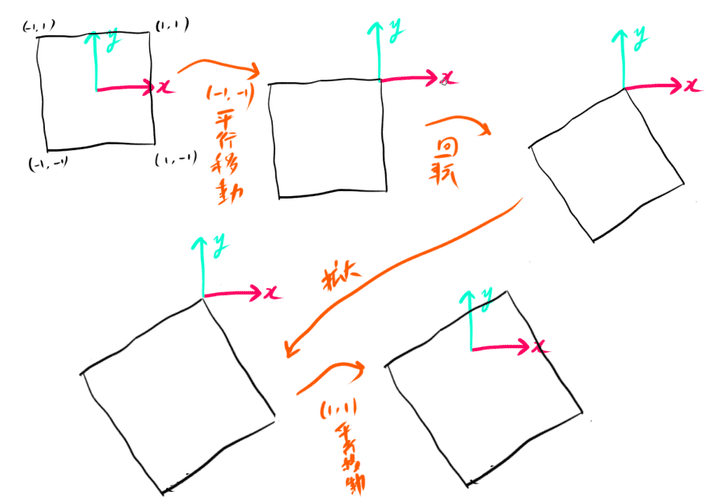
式にすると次のとおりです。

$\begin{aligned} \left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right) =& \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{array} \right)\\ &\;\;\; \left( \begin{array}{ccc} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right) \end{aligned}$

---

ここまで話を簡単にするために2次元で進めてきました。 ここで3次元についても考えておきましょう。

$x$方向に$S_x$倍、$y$方向に$S_y$倍、$z$方向に$S_z$倍にする拡大行列は次のとおりです。

$\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

次は回転について考えてみます。

$x$軸を中心に$\theta$度回転させる回転行列は次のとおりです。

$\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

$y$軸を中心に$\theta$度回転させる回転行列は次のとおりです。

$\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

$z$軸を中心に$\theta$度回転させる回転行列は次のとおりです。

$\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

最後に平行移動について考えてみます。 $x$軸方向に$T_x$、$y$軸方向に$T_y$、 $z$軸方向に$T_z$だけ平行移動する拡大行列は次のとおりです。

$\left( \begin{array}{c} x' \\ y' \\ z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

3次元の場合もこれらの行列の積によって複雑な変換を表現できます。

---

Model行列

ここで改めてモデル変換について考えます。 モデル変換はモデルのローカル座標をワールド座標に変換するものです。 モデルのx軸y軸z軸方向の拡大縮小と回転、そして平行移動について考えます。

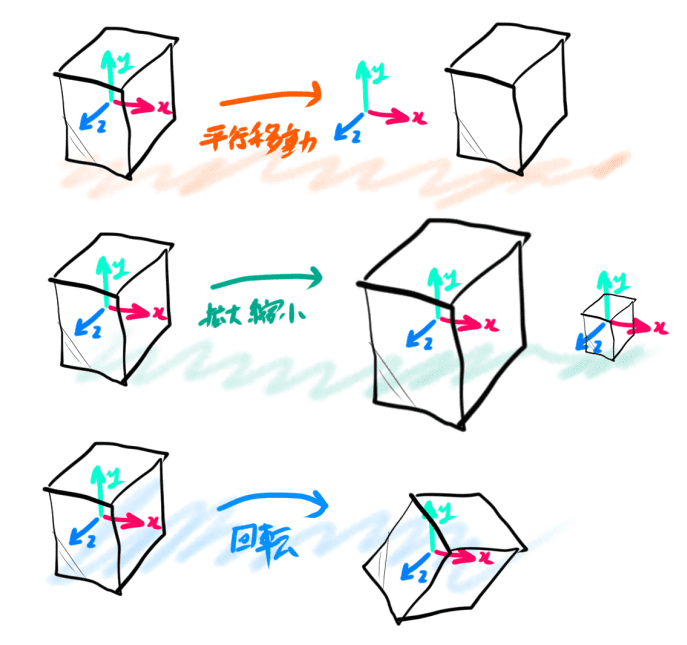
ちょうどUnityのTransformで行える変換ですね。

これは次のような行列で表せます。

$\left( \begin{array}{cccc} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{cccc} R_{11} & R_{12} & R_{13} & 0 \\ R_{21} & R_{22} & R_{23} & 0 \\ R_{31} & R_{32} & R_{33} & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{cccc} S_x & 0 & 0 & 0 \\ 0 & S_y & 0 & 0 \\ 0 & 0 & S_z & 0 \\ 0 & 0 & 0 & 1 \end{array} \right)$

これを計算した結果の次の行列について考えます。

$\left( \begin{array}{cccc} m_{11} & m_{12} & m_{13} & T_x \\ m_{21} & m_{22} & m_{23} & T_y \\ m_{31} & m_{32} & m_{33} & T_z \\ 0 & 0 & 0 & 1 \end{array} \right)$

左上の$3×3$成分が拡大縮小と回転を表していて、 右側の$(Tx, Ty, Tz)$が平行移動成分になっています。 4行目は$(0, 0, 0, 1)$で固定になります。

この行列でモデルのローカル座標からワールド座標に変換できることがわかりました。 このモデル変換を行う行列のことをモデル行列と呼んだりします。

Unityではシェーダ内でunity_ObjectToWorldという変数でこの行列にアクセスできます。 オブジェクトのローカル座標からワールド座標に変換するということで こういう名前がついています。

---

View行列

モデル変換によってモデルのローカルの座標からワールド座標に変換できました。 しかし、ワールド座標のままレンダリングは行なえません。 3DCGをレンダリングする際にはカメラから見てどこに頂点があるかというのが重要になります。 このカメラから見た相対座標のことをカメラ座標といったりアイ・スペースと呼んだりします。 このカメラからみた相対座標を求めるために、ワールド座標からカメラ座標に変換するのが ビュー変換となります。

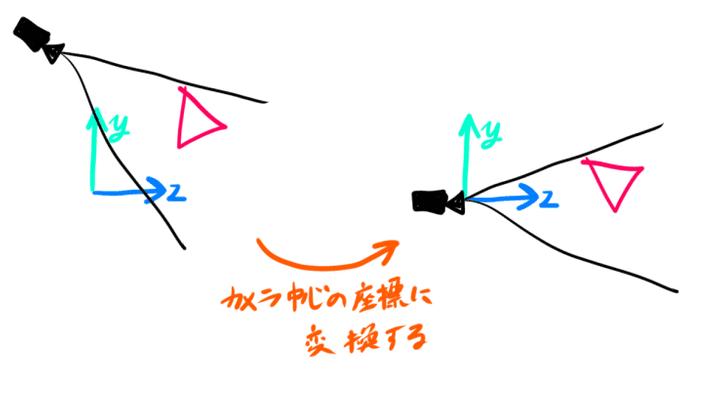
ビュー変換は、カメラの位置と回転が与えられたときに、 それと逆方向の変換になります。

説明を簡略化するために2次元で説明します。

カメラが$z$方向に$T_z$、$y$方向に$T_y$平行移動したときについて考えてみます。

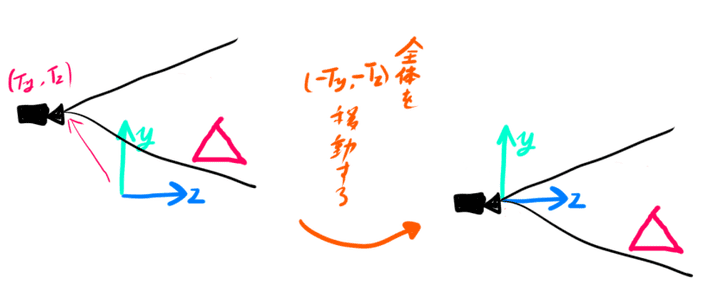
この場合、カメラ座標はワールド全体を$z$方向に$-T_z$、 $y$方向に$T_y$平行移動したものになります。

カメラの変換と逆方向に動かしてカメラを原点に持っていくことで ワールド座標からカメラ座標を求められるということですね。

カメラを$\theta$回転させた場合を考えてみます。

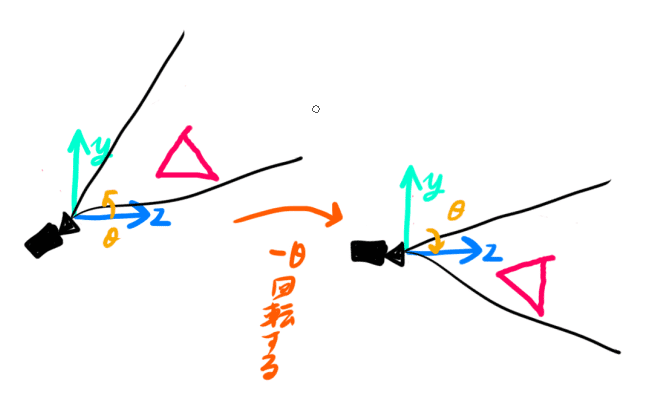
これもワールド全体にカメラの変換を戻す変換をかけることで ワールド座標からカメラ座標を求められます。

カメラが$\theta$回転し$(T_y, T_z)$移動した場合についても考えてみます。

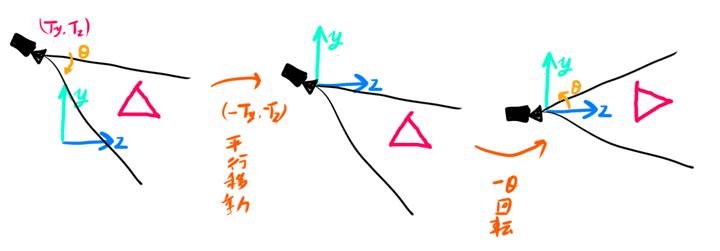
この場合も同様に逆方向の変換をワールド全体にかけてあげればよいことになります。

カメラの変換には拡大縮小は考えません。 カメラの回転と位置の逆方向の変換がビュー変換となります。

回転と平行移動が行列で表現できることは説明しました。 ビュー変換を表現する行列のことをビュー行列と呼びます。

Unityのシェーダ内ではUNITY_MATRIX_Vというビュー行列を取得できます。

---

Projection行列

MVP行列の最後の要素はProjection行列です。

Projection行列はいわゆるパースを扱うものになります。 最初にパースのかかった投影について軽く説明をします。

絵を描くにも3DCGを表示するにも3次元の物体を2次元に落とし込む作業が必要になります。 この3次元を2次元に落とし込む方法のことを投影といいます。 主だった投影方法には、透視投影と平行投影の2種類があります。 ここでは透視投影について説明をします。

透視投影のわかりやすい例はピンホールカメラです。

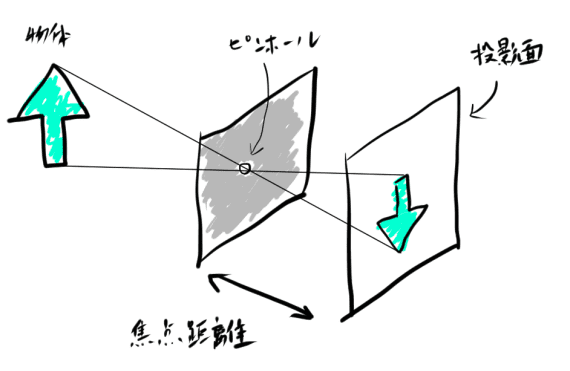
大きさを無視できるピンホールを使うことで、光の直進性により投影面に像ができます。 この像は近くのものは大きく遠くのものは小さく写ります。

ピンホールを通る光の量が少ないので、実際の撮影を行うカメラでは ピンホールの代わりにレンズを用いて像を作ります。

3DCGの投影の計算においては ピンホールの位置を目やカメラの位置（視点）とし、 視点より前に投影面を置きます。

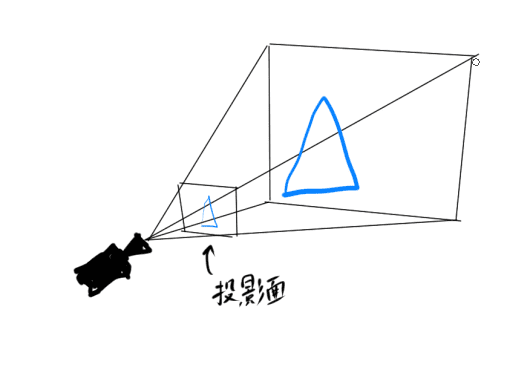
ピンホールカメラでは投影面は視点より後ろでしたが、 これだと像が上下左右逆になって扱いにくいため 3DCGで投影の計算を行う際には投影面は視点の前に置きます。

平面$z=1$を投影面としたときの$yz$座標の図は次のようになります。

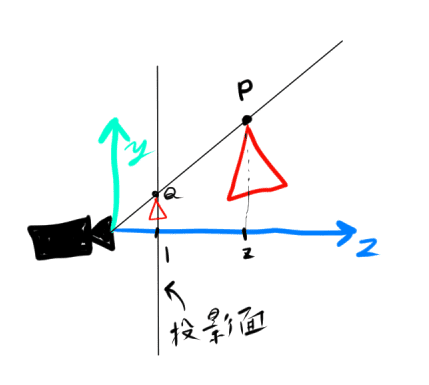
三角形の頂点$P$は$Q$に投影されます。 $P$の$yz$座標を$(y, z)$、$Q$の$yz$座標を$(y', 1)$とすると、 三角形の相似から$y:z=y':1$となります。 $x$座標についても同様なので、投影面上の点$(x', y')$は次のようになります。

$\begin{cases} x' = \frac{x}{z} \\ y' = \frac{y}{z} \end{cases}$

実際に投影の計算をする際には、投影面上に長方形を考え、 その範囲に投影される図形のみを描きます。 この長方形をウィンドウといいます。

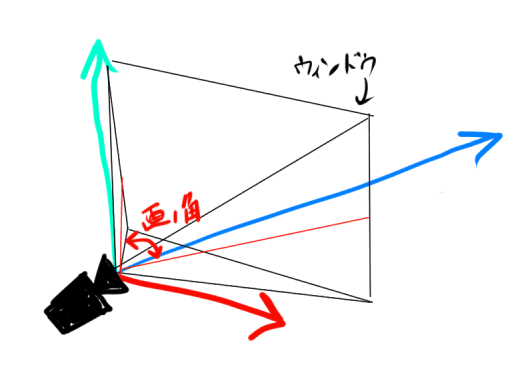
ウィンドウの大きさに合わせて視点からウィンドウをカバーする角度である画角を考えます。 画角が小さいと狭い範囲しか描画されません。 画角が大きくなると広い範囲が描画され遠近感が強調されます。

3DCGにおける透視投影はレンズの近くのものから無限遠まで描画することはなく、 前後にクリッピングした視錐台と呼ばれる領域の内部のもののみを描画します。 前後にクリッピングした面のうち視点に近いものを前方クリッピング面とよび、 視点から遠いものを後方クリッピング面とよびます。

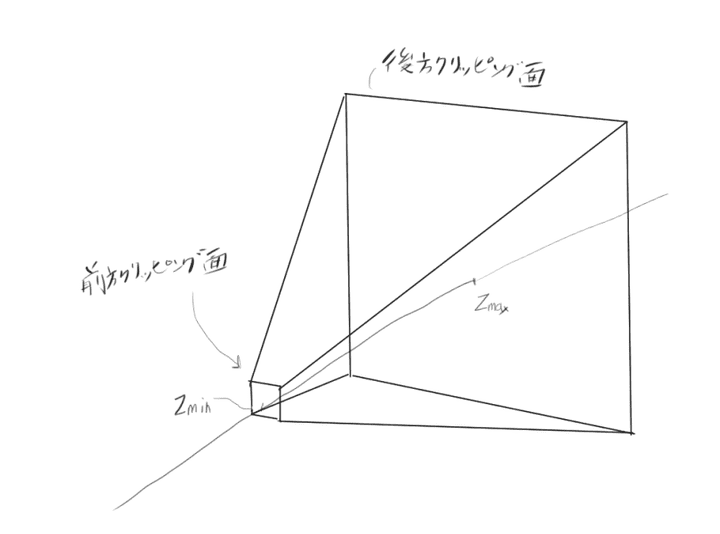
3DCGではラスタライザに渡された頂点座標を平面$x=\pm1$、$y=\pm1$、$z=0$、$z=1$で 囲まれた直方体でクリッピングして、その範囲のものだけを表示します。

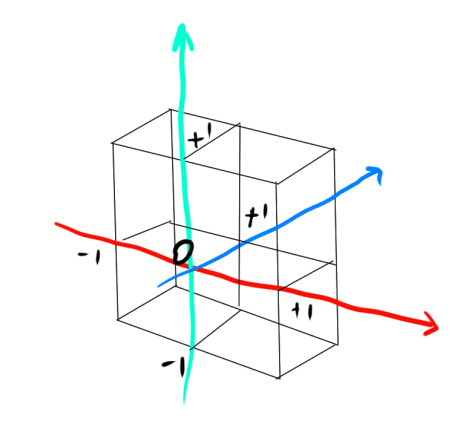
この直方体の範囲がクリッピングされ描画される範囲になります。

Projection変換はさきほどの視錐台をクリッピングの直方体に押し込む変換だといえます。 押し込んだあとの座標系を投影座標系と呼びます。

このProjection変換は、ビューボリュームの正規化する変換と 正規化ビューボリュームを透視投影する変換を行います。

ビューボリュームの正規化は、後方クリッピング面が$z=1$に、$z=1$での$x$、$y$の範囲がちょうど $-1 \le x \le 1$、$-1 \le y \le 1$になるように もとのビューボリュームを拡大・縮小するものです。

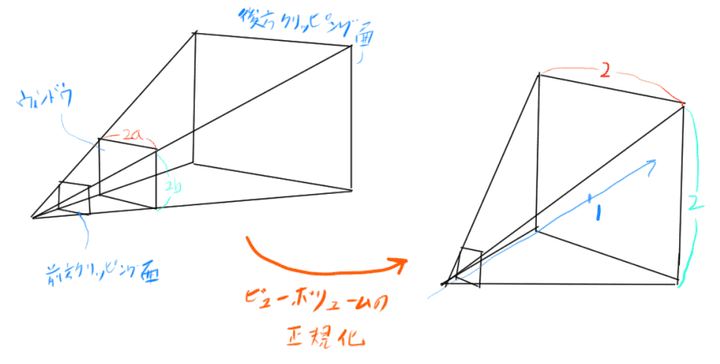
ウィンドウの横幅が$2a$でウィンドウの縦幅が$2b$のとき、 ビューボリュームを正規化する変換を行列で表すと次のようになります。

$\left( \begin{array}{c} X' \\ Y' \\ Z' \\ 1 \end{array} \right) = \left( \begin{array}{cccc} \frac{1}{az_{max}} & 0 & 0 & 0 \\ 0 & \frac{1}{bz_{max}} & 0 & 0 \\ 0 & 0 & \frac{1}{z_{max}} & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

次に正規化ビューボリュームを透視投影する変換を考えます。 $\tilde{z}_{min}=\frac{z_{min}}{z_{max}}$と置くと 透視投影の行列は次のようになります。

$\left( \begin{array}{c} X' \\ Y' \\ Z' \\ W' \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{1}{1 - \tilde{z}_{min}} & -\frac{\tilde{z}_{min}}{1 - \tilde{z}_{min}} \\ 0 & 0 & 1 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right)$

$x'$と$y'$についてはちゃんと${z}$で除算されていることが確認できます。

$\begin{cases} x' = \frac{X'}{W'}=\frac{x}{z} & \\ y' = \frac{Y'}{W'}=\frac{y}{z} & \end{cases}$

$z'$の値は次のようになります。

$z'=\frac{Z'}{W'} = \bigg(\frac{1}{1 - \tilde{z}_{min}}z -\frac{\tilde{z}_{min}}{1 - \tilde{z}_{min}}\bigg)\frac{1}{z} = \frac{1}{1 - \tilde{z}_{min}} - \frac{\tilde{z}_{min}}{1 - \tilde{z}_{min}}\frac{1}{z}$

$z=\tilde{z}_{near}$で$z'=0$に、$z=1$で$z'=1$になることが確認できます。

ビューボリュームの正規化と透視投影を行う行列を合わせた Projection変換を行う行列をProjection行列と呼びます。 Unityではシェーダ内でUNITY_MATRIX_Pという変数で受け取ることができます。

MVP行列

MVP行列と呼ばれるものはModel行列、View行列、Projection行列をかけ合わせたものです。

$MVP = P * V * M$

モデル行列はモデルのローカル座標をワールド座標に変換するものでした。

ビュー行列はワールド座標をカメラから見た相対座標であるカメラ座標に変換するものでした。

プロジェクション行列はカメラ座標を投影座標に変換するものでした。

頂点シェーダ内でモデル座標から投影座標系に変換し、 ラスタライザでクリッピング座標の$x=\pm1$、$y=\pm1$、$z=0$、$z=1$の直方体の範囲内のものを ラスタライズし、フラグメントシェーダに渡します。

頂点シェーダ内で入力された頂点座標にMVPを掛けて次のステージに渡すのは このクリッピングの座標変換を行っていたのでした。

---

UnityのShader内ではMVP行列はUNITY_MATRIX_MVPという変数で受け取れます。

頂点シェーダ内にmul(UNITY_MATRIX_MVP, v)と記述すると、 Shaderファイルを保存した際にUnityObjectToClipPos(v)と直されます。 UnityObjectToClipPos(v)はmul(UNITY_MATRIX_MVP, v)より効率がよいので 修正されるようですが、やっていることは同じことです。

これで前回の記事で解説を飛ばした頂点シェーダ内のプログラムについて解説ができました。

おわりに

今回は前回の記事の頂点シェーダ内で行っていた座標変換について解説しました。

わかりにくいところや間違いなどがあれば私のTwitterアカウント(@MatchaChoco010)まで連絡をお願いします。